いきなりOpenFOAM (18)
マグヌス効果の解析(複素解析)
マグヌス効果
回転する物体に、回転軸と直交する方向に流れが当たると、物体は流れの方向および回転軸に直交する方向に力を受けます。この効果をマグヌス効果と呼びます。マグヌス効果は、野球のカーブボールなど身近に見られる現象で、ドイツの科学者H・G・マグヌスが砲弾の運動に関して、この現象の研究を行ったことに由来しています。
マグヌス効果は、実験あるいはCFDによる解析により確認できますが、理想流体(粘性、圧縮性のない流体)であれば、複素解析により比較的簡単に計算できます。
今回はOpenFOAMの解析から少し離れますが、回転する円柱周りの流線と揚力係数を複素解析により求めてみます。OpenFOAMでの計算は次回紹介します。
理想流体の複素解析
理想流体はポテンシャル流れとして扱うことができ、ポテンシャル流れは複素数を用いて表現することができます。ポテンシャル流れの説明については割愛しますが、計算方法だけ簡単に記すと、回転する円柱周りの複素ポテンシャル分布を計算し、計算された複素ポテンシャルの虚部が同じ値同士の座標を結ぶと流線が得られます。回転する円柱周りの複素ポテンシャルは下記で表されます。
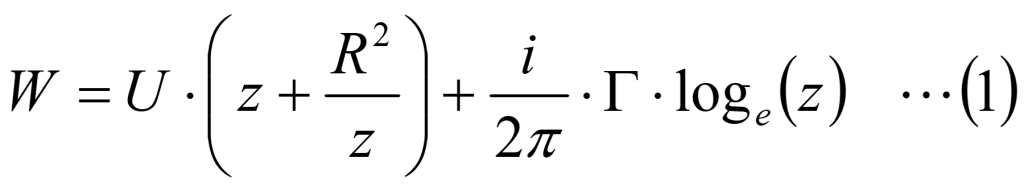
ここで、Uは一様流の流速[m/s]、Rは円柱の半径[m]、Γは循環[m2/s]、zは座標の複素表示で、z=x+i*yです。また、円柱の回転速度をω[rad/s]とすると、循環は対象を囲む積分となるため、回転する円柱の循環は、
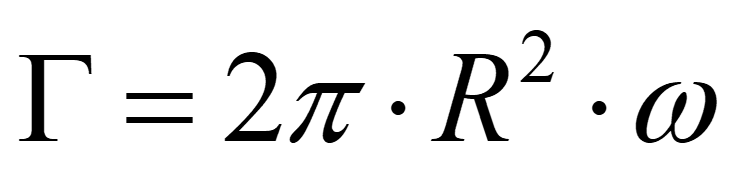
となります。
複素解析と可視化
流体力学のポテンシャル流れ解析は、複素数を用いた式を解析して現象を理解することにあり、可視化作業は手間がかかるため、結果を可視化することはあまり行われてはいませんでした。しかしながら、MATLABに代表されるエンジニアリングソフトを用いることにより比較的容易に結果を可視化できます。今回はプログラミング言語のPythonを用いて可視化する例を紹介します。
なお、プログラムの実行にはPython本体に加え、Numpy, Matplotlibを入手しインストールする必要がありますが、コードの動作確認(結果表示)であれば、ProjectJupyterなどのブラウザ上で動作するPythonの統合開発環境で試すことができます。
下記が円柱周りの流線を表示するPythonのサンプルコードです。
import numpy
from matplotlib import pyplot
pi=numpy.pi
G=2*pixy=numpy.arange(-3,3,0.01)(x,y)=numpy.meshgrid(xy,xy)z=x+1j*y
W=(z+1/z)+1j*G/2/pi*numpy.log(z)
psi=W.imag
psi=numpy.where(numpy.abs(z)<=1,0,psi)
pyplot.contour(x,y,psi,levels=numpy.arange(-4,4,0.2))
zz=numpy.exp(1j*numpy.linspace(0,2,100)*pi)
pyplot.plot(zz.real,zz.imag)
pyplot.gca().set_aspect('equal')
pyplot.show()
上記コードの4行目、Gの値が循環Γで、8行目が(1)式です。このコードでは、U=1、R=1としています。続く9行目で虚部を取り出し、11行目で塗りつぶしなしのコンターマップを描かせています。なお、等値線の間隔は11行目のlevels=~で設定しています。ここを書き換えることで、等値線の間隔を変更できます。なお、Pythonの文法やその他については割愛します。
周囲流れと回転する円柱の周速が等しい場合、循環はΓ=2πとなります。上記のコードでG=2*piとして、計算させると、図1に示す流線が得られます。図を見ると、円柱上部で流線が密となり、流速が増加していることがわかります。一方、円柱下部で流線が疎となり、流速が低下していることがわかります。ベルヌイの定理により流速の増加とともに圧力が低下することから、円柱上部では圧力が低下、円柱下部では圧力が上昇し、結果として、円柱には上向きの力が働くことがわかります。
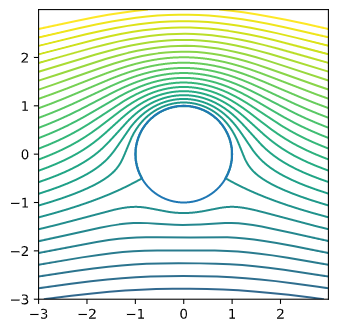
次に、循環が0の場合、図2に示すように、上下左右対称の流線となります。図2で流線は左右対称となるということは、流れが左から右であろうと、右から左であろうと結果が同じで、一見、物体は流れから抵抗を受けないという非現実的なことになり、これはダランベールのパラドクスと呼ばれています。

上述のコードで揚力係数が1となる場合の流線を求めてみます。揚力係数は下記の式で求められます。
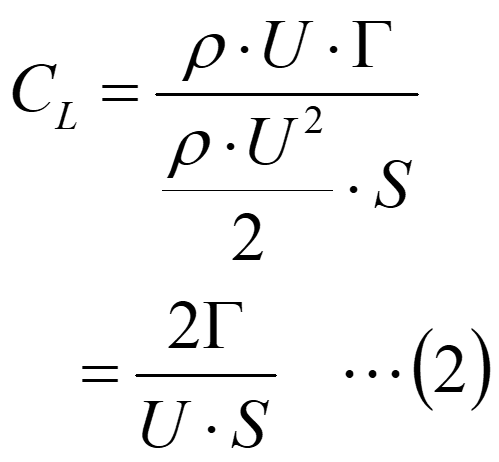
ここで、ρは流体の密度、Uは流速、Sは円柱を上から見た投影面積です。円柱の半径をR、長さをbとすると、 S=2Rbとなり、ここで、U=1、R=1、b=1とすると、CL=Γとなります。つまり、揚力係数が1の流線は上述のコードでG=1として計算すれば得られ、図3に示すような形状となります。
流線は全体的に上に凸となり、円柱上部は下部よりも流線の間隔がわずかですが狭くなっていることがわかります。

今回は理想流体におけるマグヌス効果を複素解析の例で紹介しました。
次回は、揚力係数が1となるような回転する円柱モデルを設計し、設計したモデルをOpenFOAMで解析するとともに、今回の複素解析とOpenFOAMの計算結果を比較し、理想流体と実在流体との違いを見てみます。
おことわり
本コンテンツの動作や表示はお使いのバージョンにより異なる場合があります。
本コンテンツの動作ならびに設定項目等に関する個別の情報提供およびサポートはできかねますので、あらかじめご了承ください。
本コンテンツは動作および結果の保証をするものではありません。ご利用に際してはご自身の判断でお使いいただきますよう、お願いいたします。

