いきなりOpenFOAM (23)
層流モデルと乱流モデルによる違い
層流と乱流
流れの計算を行う場合、その流れが層流なのか乱流なのかによって、計算に使用する式(モデル)を変える必要があります。一方で、層流か乱流かを判断する指標となるのがレイノルズ数ですが、いくつから乱流というようなはっきりした境目があるわけではなく、また計算する物体によっても異なります。1つの例として、円筒管内の流れでは、レイノルズ数が2,300~4,000で層流から乱流へ遷移することが知られています。その他平行平板内の流れでは350,000~1,000,000、流れの中の球だと200,000~500,000(代表長さを球の直径とした場合)で、層流から乱流に遷移します。
前回(第22回)は、抗力係数と揚力係数へのレイノルズ数の影響を見るために、流速を変化させて解析を行いましたが、その際、低いレイノルズ数の状態に対しても乱流モデル(k-εモデル)を使っていました。そこで、今回は、レイノルズ数950での解析を層流モデルと乱流モデル(k-εモデル)を使って解析を行い、結果を比較してみます。
条件の変更
これまで、XSimでの条件設定では、常に乱流を設定してきましたが、層流モデルでの計算は基本設定の「乱流」のチェックを外すだけです。
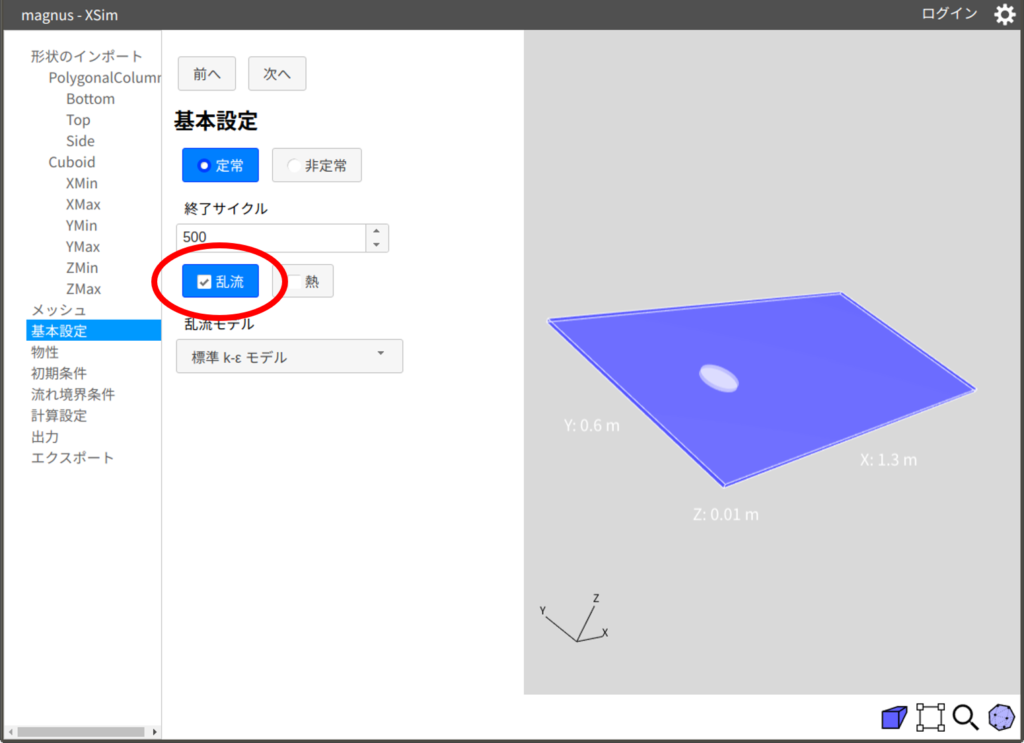
その他の設定については、第21回を参考にしてください。
ParaViewでの結果の可視化
レイノルズ数950での解析結果を図2から7に示します。偶数番は層流モデルで、奇数番はk-εモデルでの計算結果です。図を見ると、流速分布、静圧分布、境界層の形状ともに、層流モデルでの計算結果とk-εモデルでの計算結果とは非常によく似ています。

図2 流速分布(層流モデル) 
図3 流速分布(k-εモデル)

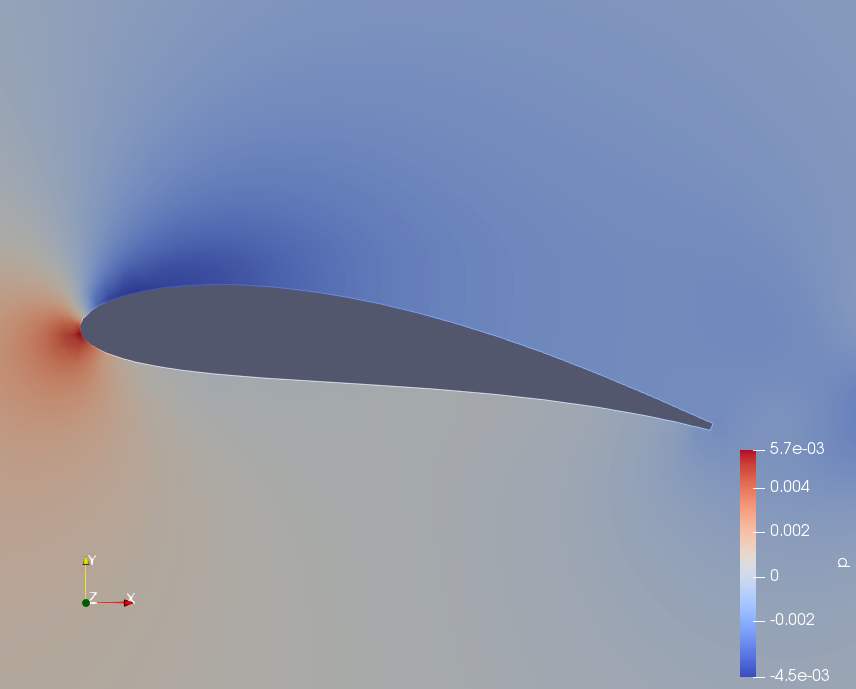
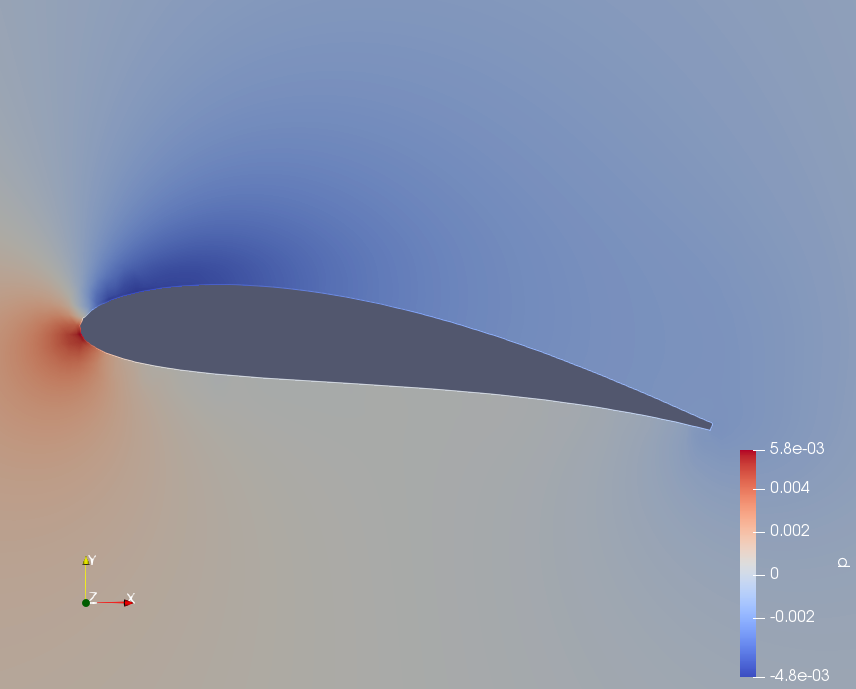
図4 静圧分布(層流モデル) 
図5 静圧分布(k-εモデル)

図6 速度境界層形状(層流モデル) 
図7 速度境界層形状(k-εモデル)
postProcessingフォルダ内のforceCoeffs.dat内の抗力係数と揚力係数を読み取って、比較した結果が表1です。表を見ると、層流モデルの抗力係数・揚力係数は、k-εモデルのそれよりも多少小さくなりますが、ほぼ同じ値となっています。小数第一位までの精度が必要とすると、どちらのモデルを使っても同じ結果が得られることになります。計算する対象によるため一概には言えませんが、低レイノルズ数の解析で、層流モデルと乱流モデルのどちらを使うかについては、それほど神経質にならなくても良いと言えます。
| 層流モデル | k-εモデル | |
| 抗力係数 Cd | 0.198 | 0.202 |
| 揚力係数 Cl | 0.563 | 0.611 |
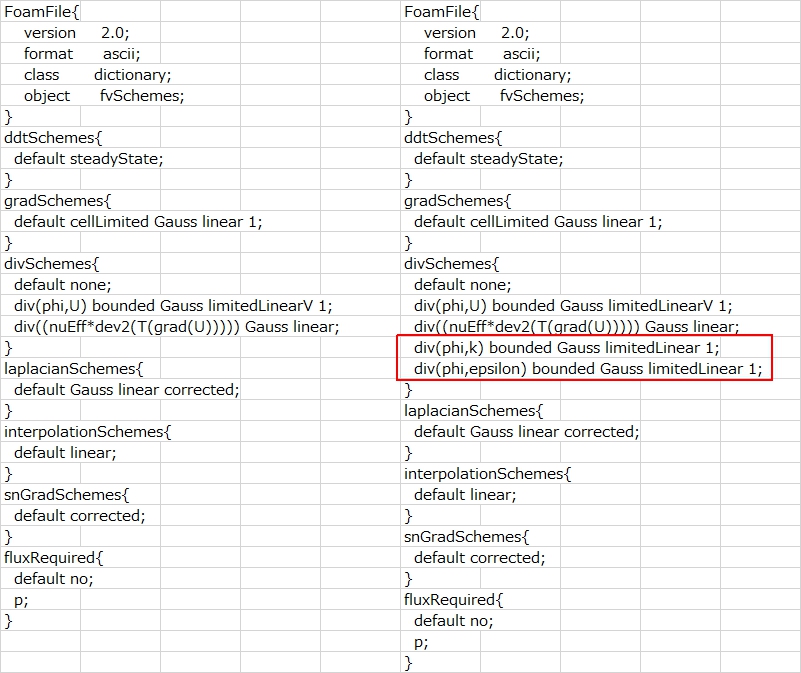
さて、層流モデルと乱流モデルでは、OpenFOAM内ではどのように異なるのでしょうか? ここでは大まかな説明となりますが、簡単に説明します。層流モデルと乱流モデルとでは、OpenFOAMに対して、計算の方法を指示するsystemフォルダ内のfvSchemes内の記述が変わります。図8はfvSchemes内の記述で左側が層流モデルを設定した場合で、右側がk-εモデルを設定した場合です。図の赤い枠が異なる部分で、k-εモデルでは、kとepsilonに関する処理が追加されています。この他、緩和係数や初期設定などでも、k-εモデルではkとepsilonに関する追加があります。
CFD内では下記のナビエ・ストークスの式(非圧縮性、外力なし)を数値的に解いています。
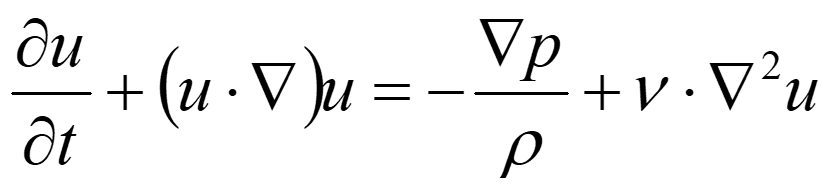
ここで、uは流速ベクトル、pは静圧、ρは密度、νは動粘性係数です。
上記はベクトル表記ですが、わかりやすくx,yの2成分として、x軸方向のみを表示すると、
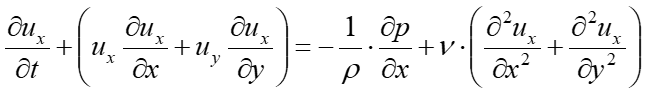
となります。
ナビエ・ストークスの式の左辺第1項は加速度項、左辺第2項は流体では速度は時間と空間とに依存するための項で、移流項と呼ばれています。右辺第1項は圧力勾配項で、右辺第2項は粘性項です。
物体表面では流れは静止しているため、物体表面近傍では速度変化が大きくなり、粘性項の影響が大きくなります。動粘性係数は流体の物性値であり、一定値となりますが、乱流状態では見かけ上、粘性が変化します。これは渦粘性係数と呼ばれ、流れの状態によって変化します。詳細は省きますが、k-εモデルでは、乱流をエネルギーのバランスで捉え、乱流エネルギーkと散逸率εの2つの変数で渦粘性係数を求めています。
つまり、図8の赤枠部分で渦粘性を求めているかどうかが、層流モデルと乱流モデルとの違いになります。今回の計算では、流速が遅く、この違いが小さくなったことで、結果的に(偶然に)差が小さくなったものと考えられます。元々k-εモデルは高レイノルズ数を前提としたモデルであるため、低レイノルズ数の流れでは正確に計算されているとは言えず、明らかに層流状態となるものに対しては層流モデルを使う必要があります。一方、工学系の大部分の現象は乱流状態であり、とりあえずは乱流モデル(k-εモデル)で解析を行い、結果を見てから判断するというのも現実的な選択です。
今回は、ジューコフスキー翼のモデルを用いて、層流モデルと乱流モデルで抵抗係数と抗力係数が変化するかを確認しました。次回は、翼形状が一定間隔で並んでいる翼列の計算をしてみます。
今回、各アプリケーションの操作説明は省略しています。FreeCADの具体的な操作については、いきなりOpenFOAM第5回および第7回、OpenFOAMでの計算実行は第8回、ParaViewの操作については第3回、第4回および第8回を参考にしてみてください。
おことわり
本コンテンツの動作や表示はお使いのバージョンにより異なる場合があります。
本コンテンツの動作ならびに設定項目等に関する個別の情報提供およびサポートはできかねますので、あらかじめご了承ください。
本コンテンツは動作および結果の保証をするものではありません。ご利用に際してはご自身の判断でお使いいただきますよう、お願いいたします。