いきなりOpenFOAM (38)
堰を越える流れ(その3)
水理学からのアプローチ
前回は堰を越える流れをOpenFOAMで解析してみました。流れには、水深が深く遅い流れの常流と水深が浅く速い流れの射流とがあることが解析結果を可視化することで確認できましたが、汎用的に整理できれば、より応用範囲が広がります。水路内の流れを解析する手法が水理学です。水理学全体を網羅することは紙数の関係で難しいため、今回は、堰を越える流れについて、水理学の手法を説明し、前回の解析結果と比較してみます。
図1は、堰を越える流れを模式的に示したものです。図において、左から流速VAで流入した流れが高さZの堰を越えるとします。破線が水面です。
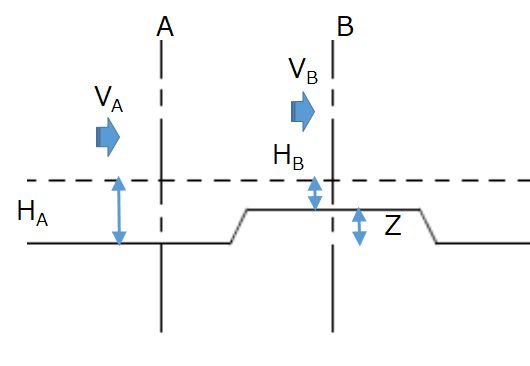
ベルヌイの定理から、Aの位置における全圧とBの位置における全圧は等しくなるため、下記の式が成り立ちます。
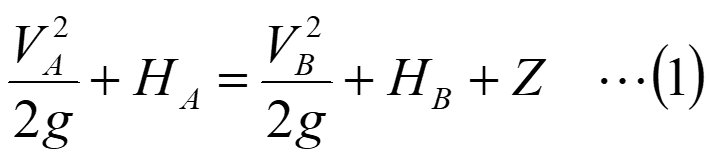
ここで、Vは流速[m/s]、Hは水深[m]、Zは水路底面高さ[m]、gは重力加速度[m/s2]です。水理学における圧力の単位は、水頭あるいはヘッドと呼ばれる水注高さを用い、Pa単位の値を重力加速度と密度との積で割った値を用います。水頭の単位はmです。したがって、動圧項は
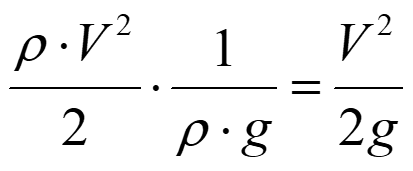
となります。また、静圧項は水面高さとなります。
ここで、動圧分と水深に相当する静圧分との和を考えます。これは、全水頭から水路底部高さZを差し引いたもので、比エネルギーと呼ばれます。比エネルギーEは下記の式で表されます。
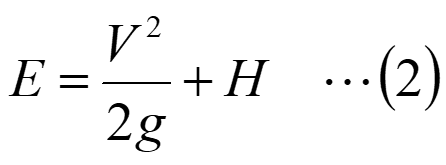
また、流量をQ[m3/s]、水路幅をB[m]とすると、(2)式は
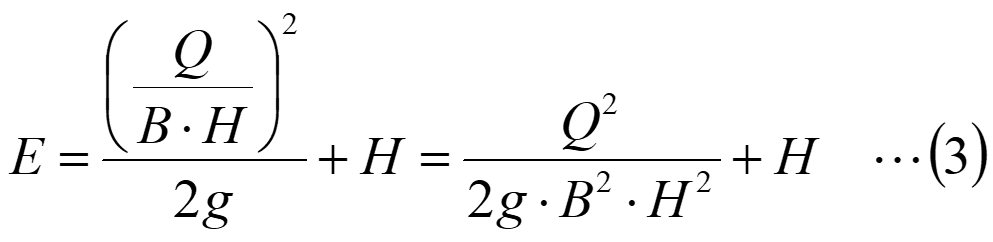
となります。
ここで、水路幅Bは一定とすると、流量Qも水路に沿って一定であるため、比エネルギーEは水深Hのみの関数となります。流量Q=1m3/min、水路幅B=1mとして、比エネルギーEを水深Hとをプロットしてみると、図2に示すように、比エネルギーEは水深Hの増加とともに減少し、ある水深を超えると、水深の増加とともに比エネルギーも増加することがわかります。
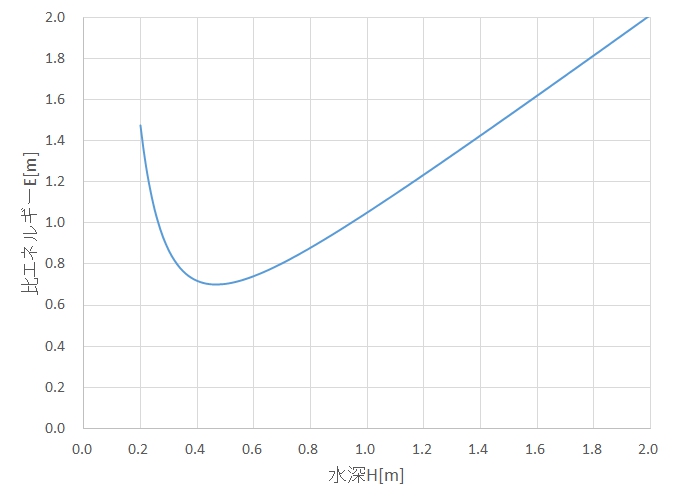
図で、比エネルギーが最小となる水深が限界水深と呼ばれます。限界水深Hcでは、(3)式の比エネルギーEを水深Hで微分したdE/dHが0となることから、限界水深Hc[m]は、流量Q[m3/s]、水路幅B[m]に対して、下記の式で求まります。
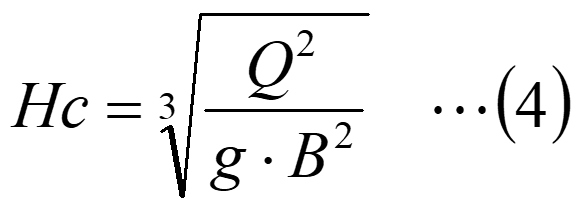
(4)式を流量Qについて解くと、限界水深Hcから流量Qを下記の式で求められます。
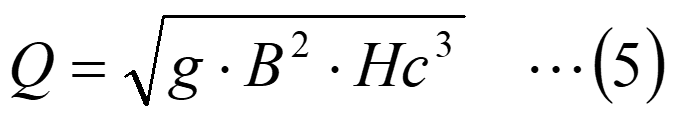
詳細は省きますが、堰を越える流れでは、堰の上部で限界水深となります。したがって、堰の高さ、水路幅、流量がわかれば、その水路での基準となる水位が(4)式から求められます。一方、水路幅と堰上の水深がわかれば、流量が(5)式から求められます。これは、堰流量計と呼ばれ、河川の流量を計測する手段として使われています。
前回の解析モデルから限界水深を計算してみます。解析モデルの緒元は、水路幅が100mm、流量が0.01m3/sであったので、限界水深は(4)式から
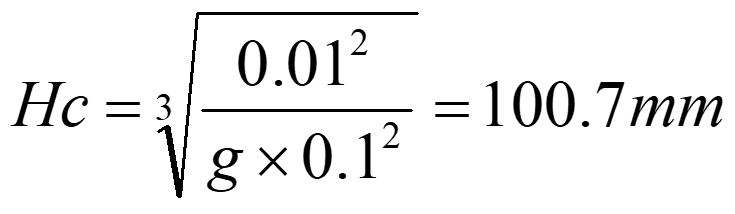
となります。
CFD解析結果との比較
前回の解析結果から、堰上部の水深を求めてみます。ParaViewの画像から堰高さなどを基準に堰上部での水深を求めてもかまいませんが、ここではParaViewのデータ出力機能を使ってみます。始めに、水路中央を通過する縦断面を作成します。次に、縦断面で、alphaが0.5の等値面を作成します。これで、縦断面での水位形状が曲線として得られます。この曲線をCSVファイルとして出力します。file→saveDataとして、拡張子はCSVを選択し、適当な名称でファイル名を設定します。OKをクリックすると、図3に示すような縦断面での水位を含んだ情報がCSVファイルとして出力されます。図において、F、G、H列がそれぞれ、水位のX座標、Y座標、Z座標となります。
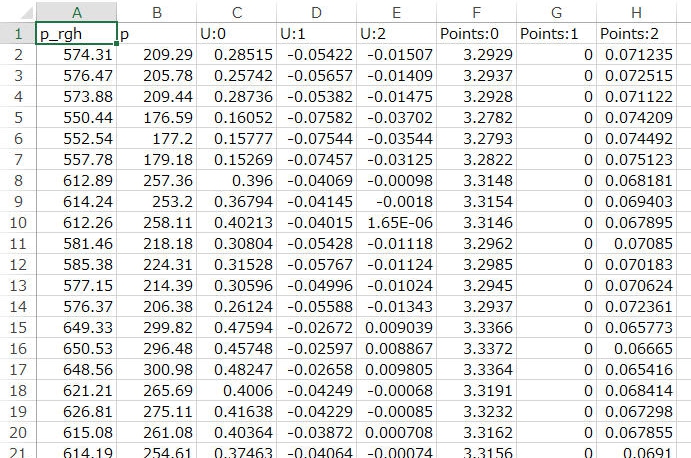
水位のX座標とZ座標とから、水面形状を作成すると、図4に示す水面高さの変化が得られます。図には橙色の線で水路底面形状も示しています。図を見ると、堰頂上の流れ方向への中間で水深を求めてみると、0.1mとなり、先ほど計算した限界水深と一致することがわかります。
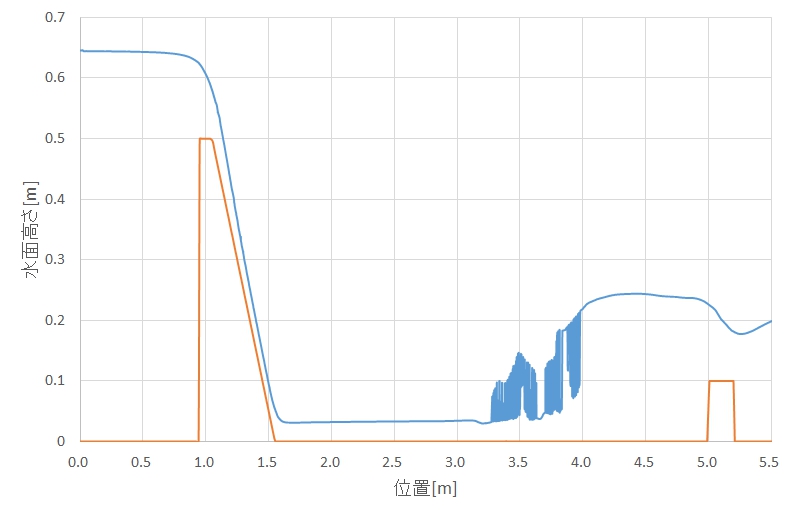
図4を見ると、堰を越えた後の流れは、水深の浅い流れの後、水深が変動し、増大しています。堰を越えた後の水深の浅い流れは射流と呼ばれています。一方、堰を越える前と後半の水深が増加している部分は常流と呼ばれています。射流から常流に移行する部分が図の水深が変動する部分で、跳水と呼ばれています。跳水は、前回の解析結果から求めた水面形状に見られるように、河川においても、水面の不規則な変動(さざ波)として現れます。
常流と射流との流れの状態はフルード数で区別できます。フルード数は下記の式で示す無次元数です。
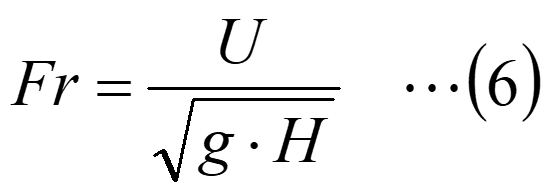
ここで、Uは流速[m/s]、Hは水深[m]、gは重力加速度9.8m/s2です。詳細は省きますが、フルード数が1未満では流れは常流となり、1を超えた流れは射流となります。フルード数が1で流れが常流から射流へ、射流から常流へと切り替わります。
図4の水面高さから水路底面を差し引いて、水深を求めた後、流量と水路幅から、流速を計算すると、流れ方向に沿ったフルード数が図5に示すように求まります。図の青い線が水深で、橙色の線がフルード数です。フルード数の変化が堰上部で1未満から1以上へと変化していることがわかります。ここで、流れは常流から射流へと切り替わっています。また、堰を超えた後、フルード数が1を超える状態が続きますが、フルード数、水深ともに不規則に変化し、フルード数が1未満へとなります。この不規則に変化する部分が、跳水が発生している個所です。
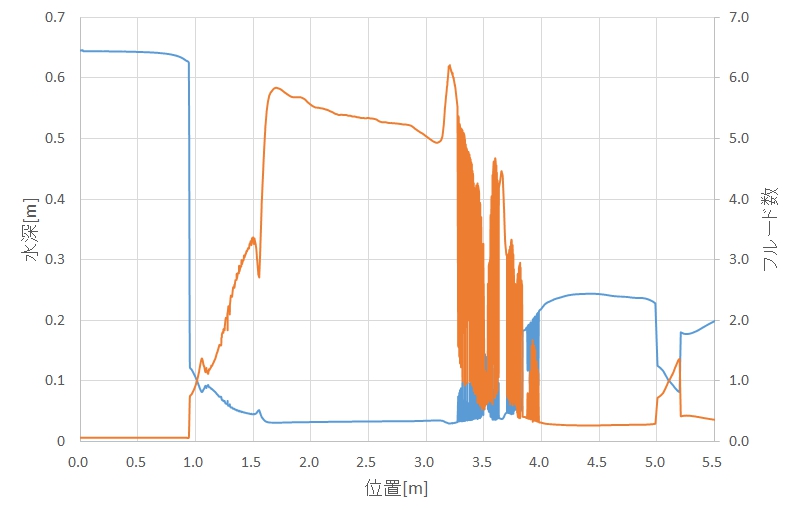
フルード数は(6)式から、流速に比例するため、例えば、意図的に水深を増加させて、流速を低下させると、フルード数を低下させることができます。前回解析のモデルで、後方に設けた小さな堰は、手前で水深を増加させることで流速を低下させ、射流から常流への移行を促進します。水路底面での摩擦損失により流速は低下するため、後方の小さな堰がなくとも、いずれ流れは射流から常流へと移行しますが、長い距離を通過するおそれがあります。現実の河川においても、ダムからの放流後の流れは射流となり、川床を削ってしまうため、同様な副ダムを設けて、常流への移行を促進させています。
詳細は省きますが、水面を伝わる波の速さC[m/s]は下記の式で表されます。
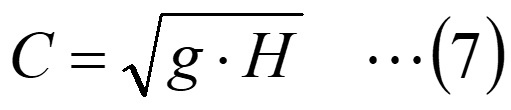
(6)式と(7)式を比べると、フルード数は流れの速さと波の速さとの比と考えられます。下流の状態は、水面を伝わる波として上流側に伝わります。流れの速さが水面を伝わる波よりも遅い場合、流れは下流の状態に依存し、これが常流です。一方、流れの速さが水面を伝わる波よりも速い場合、流れは下流の状態に依存しなくなります。これが射流です。常流から射流へは下流の状態が水面の波として伝わるため、連続的に移行しますが、射流から常流へは下流の状態が伝わらないため、どこかで破綻が生ずるまで射流の状態が続きます。これが、跳水現象です。図6の動画を見ると、後方の小さな堰で発生した波が流れにより押し戻され、水面が不規則に変動していることがわかります。
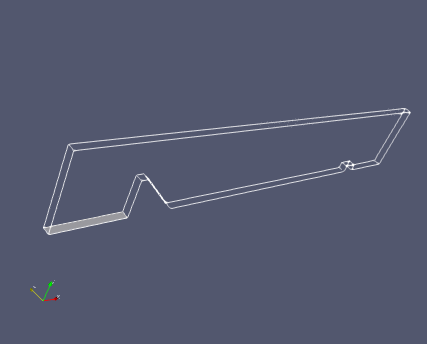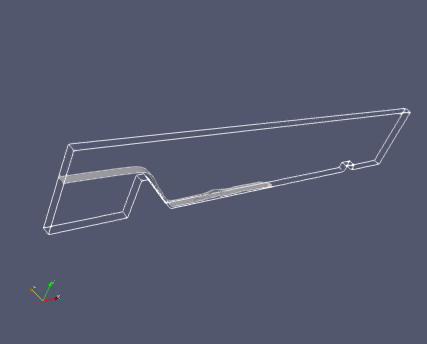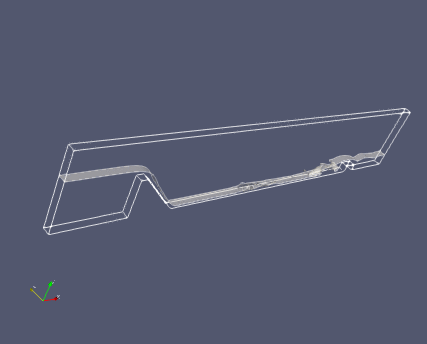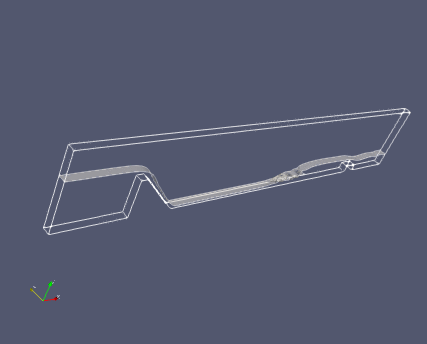
今回は、前回に引き続き堰を越える流れを水理学の側面から検証してみました。今回紹介した射流から常流への変化は、身近な例では、キッチンシンクなどで見られる水流による水膜生成として観察できます。次回は、水流による水膜生成をOpenFOAMで解析してみます。
このページでは、各アプリケーションの操作説明は省略しています。FreeCADの具体的な操作については、いきなりOpenFOAM第5回および第7回、OpenFOAMでの計算実行は第8回、ParaViewの操作については第3回、第4回および第8回を参考にしてみてください。
おことわり
本コンテンツの動作や表示はお使いのバージョンにより異なる場合があります。
本コンテンツの動作ならびに設定項目等に関する個別の情報提供およびサポートはできかねますので、あらかじめご了承ください。
本コンテンツは動作および結果の保証をするものではありません。ご利用に際してはご自身の判断でお使いいただきますよう、お願いいたします。

