いきなりOpenFOAM (50)
タンクからの液体の流出
解析モデルとメッシュ作成
前回は、逆さにした瓶からの液体の流出を解析してみましたが、もし、瓶の底が開放された状態であれば、瓶から流出する液体の流速v[m/s]は、トリチェリの定理により
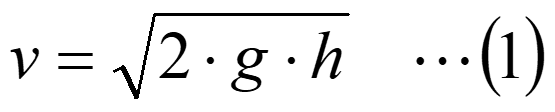
で求められます。
ここで、hは流出口から水面までの高さ[m]、gは重力加速度9.8m/s2です。トリチェリの定理はベルヌイの定理で説明できます。詳細は下記リンクを参照願います。
https://ja.wikipedia.org/wiki/%E3%83%88%E3%83%AA%E3%83%81%E3%82%A7%E3%83%AA%E3%83%BC%E3%81%AE%E5%8E%9F%E7%90%86
今回は、そのトリチェリの定理をOpenFOAMで再現してみます。
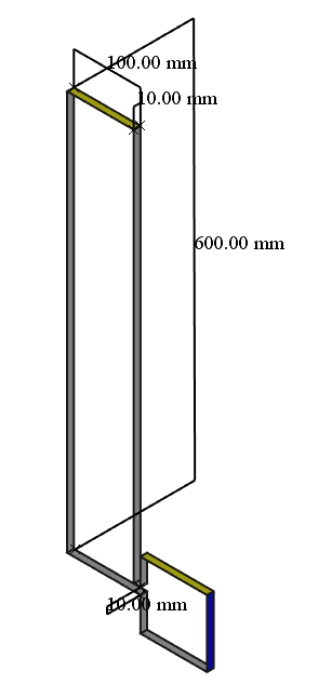
始めに、解析モデルをCADで作成します。図1に示すように、高さ600mm、幅100mm、厚さ10mmの容器の底に設けられた高さ10mmのノズルから流出するものとします。流出する様子も観察できるように、容器の流出口には幅100mm、高さ100mmの空間を接続し、図中、青色で示す空間右側面を領域outletとします。また、図中、黄色で示す容器の上部の面と容器流出口につながる空間の上面とを領域atmosphereとします。図中、灰色で示す容器の側面を領域wallsとします。その他の容器前後の面はsideとして、stlファイルを出力します。
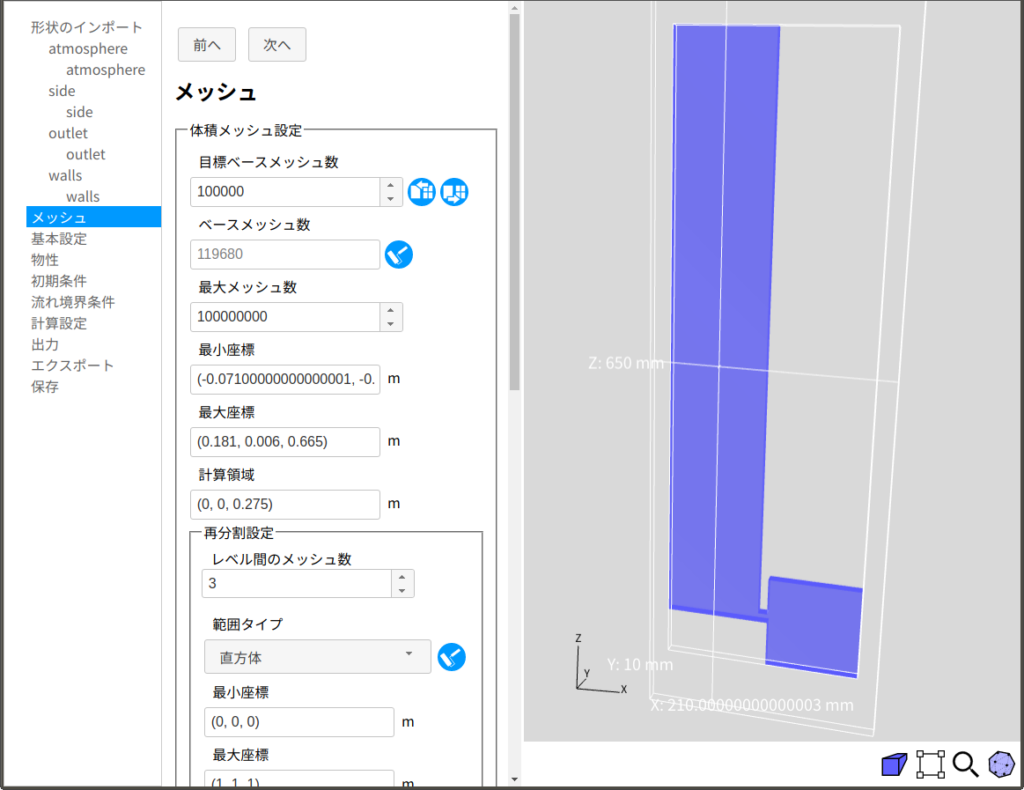
ブラウザでXSimに接続し、インポートとスケール変更を行います。メッシュ設定では、図2に示すように、目標ベースメッシュ数をデフォルトより2桁ほど多くします。計算領域は、容器の内部の点となるように座標を変更します。また、領域wallsにはデフォルト設定で境界層を設けます。次に、エクスポートで解析ファイルを出力、展開した後、コマンド./Allrun –mでメッシュを生成します。
ファイルの修正
解析ファイルは前回の「逆さにした瓶からの液体の流出」用のファイルセットを用います。コピーを作成し、計算結果や0フォルダ内のalpha.waterファイル、constantフォルダ内のpolyMeshフォルダを削除しておきます。 ./Allrun –mで出力されたconstantフォルダ内のpolyMeshフォルダを先ほどの解析用ファイルのconstantフォルダ内に移動します。領域名を変更しない場合は、setFieldsDictファイルとcontrolDictファイル以外は、そのまま流用できます。
systemフォルダ内のsetFieldsDictファイルを図3に示すように修正します。setFieldsDictファイルでは、boxToCellを用いて、液体を設定します。今回は、液面高さを500mmとしました。setFieldsDictファイル設定の詳細については、いきなりOpenFOAM第45回を参照してください。

次に、controlDictファイルを図4に示すように修正します。controlDictファイルでは、解析終了時間や計算結果の出力間隔などを設定します。時間刻みは、時間刻みの自動設定が働くため、前回の設定を流用し、必要に応じて修正する方法で構いません。controlDictファイル設定については、いきなりOpenFOAM第36回を参照してください。
なお、今回は流出量を求めるため、controlDictファイル後半にfunctionsとして、領域outletを通過する流量を出力させています。なお、ここで出力される流量は質量流量のため、一般に使われる体積流量で結果を得るには、出力結果を液体密度で割る必要があります。

ファイルを修正・上書き保存したら、端末で、setFields、interFoamの順にコマンドを入力すると、計算が始まります。
結果の可視化
計算が終了したら、paraFoamと入力し、ParaViewを起動して結果を可視化します。ParaViewの使い方や液面の表示については、いきなりOpenFOAM第34回を参照してください。
図5と図6に、流出開始から1秒後と4秒後の液面形状を示します。また、図7は液面形状の変化の動画です。図から時間経過に伴い、ノズルからの流出する液体の勢いは低下する様子が見られます。
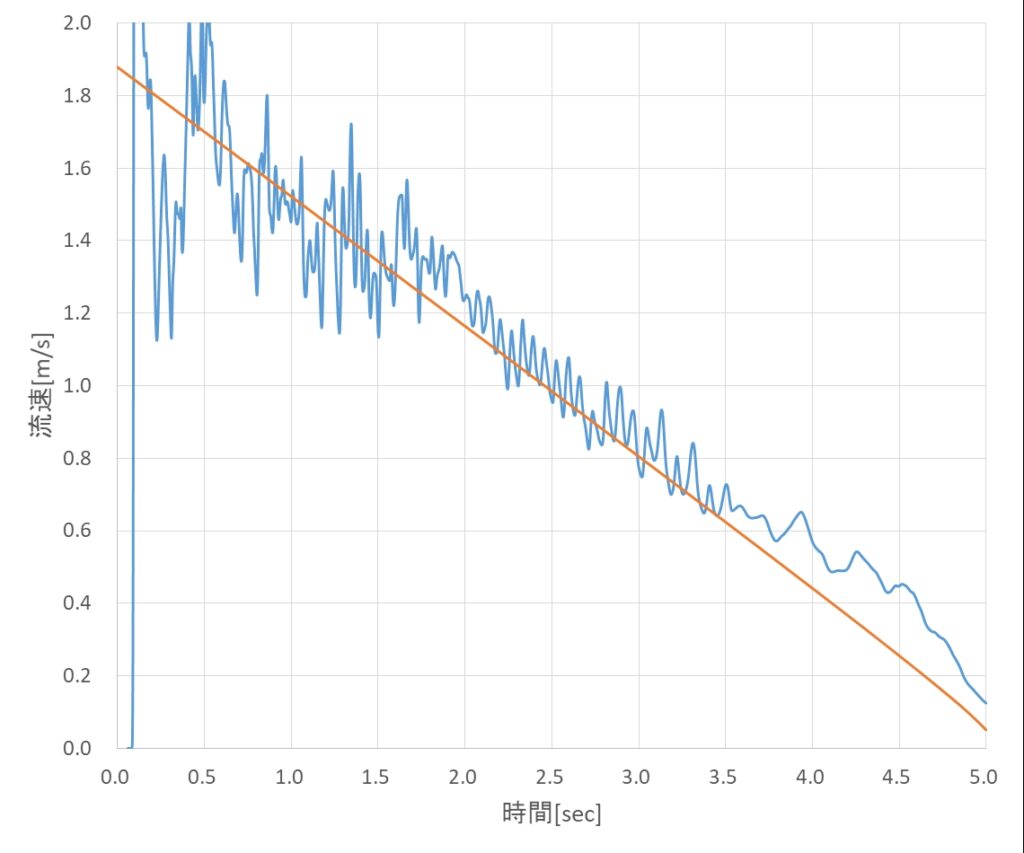
上記を定量化するために、postProcessingフォルダ内のsurfaceFieldValue.datから流出質量流量を読取り、体積流量に換算しプロットすると図8が得られます。図の橙色の線は、流出流量が液面高さの平方根に比例するとして、計算した結果です。ここで、トリチェリの定理では比例係数は√(2g)ですが、実在流体ではノズル内壁で流速の低下が起きるため、比例係数は√(2g)よりも小さくなります。図中、橙色の線は比例係数が0.6×√(2g)として計算した結果です。
マリオットの瓶を解析する
図1のモデルでは、大気圧の位置は液面となりますが、もし、大気圧の位置を液中の一定の高さに設定できれば、流出流速を液面の高さに依らず一定とできます。この考え方がマリオットの瓶と呼ばれるもので、植物への自動給水機などに使われています。
https://ja.wikipedia.org/wiki/%E3%83%9E%E3%83%AA%E3%82%AA%E3%83%83%E3%83%88%E7%93%B6
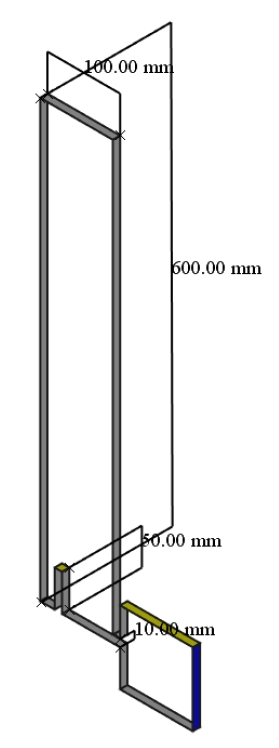
図1のモデルを修正して、マリオットの瓶をOpenFOAMで再現してみます。図9に示すように、容器底面から高さ50mmの位置に流入口を設けます。容器上面は領域wallsに変更し、流入口を領域atmosphereに設定します。
これまでと同様にstlファイルを出力し、XSimで解析ファイルを作成し、端末から./Allrun –mでメッシュを生成します。解析ファイルは、前述のファイルをコピーペーストして流用します。端末にsetFields、interFoamの順にコマンドを入力し、計算を開始し、計算が終了したら、paraFoamと入力し、結果をparaviewで可視化します。図10は流出開始から1秒後、図11は4秒後の液面の変化を示します。図を見ると、ノズルから流出する勢いは変わらないことがわかります。また、図12は液面変化の動画です。
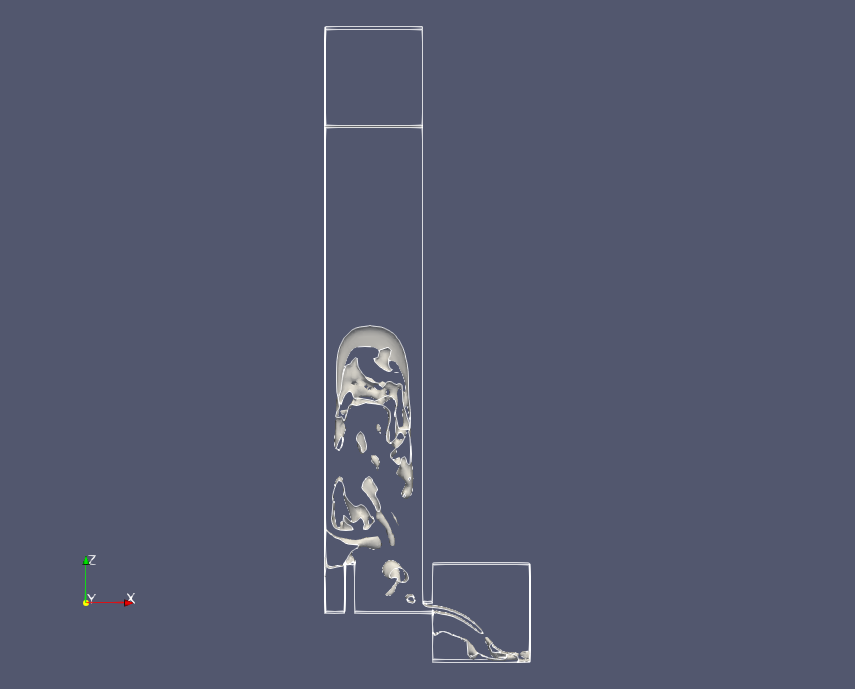

図10、11および図12の動画から、ノズルからの流出速度は液面高さによらず一定となるとみられますが、これを定量化してみます。解析結果のpostProcessingフォルダ内のsurfaceFieldValue.datから質量流量を読取り、流出速度を求めます。図9のモデルでは、容器内のatmosphereの位置は容器底から50mmの位置にあるため、トリチェリの定理から、流出速度は
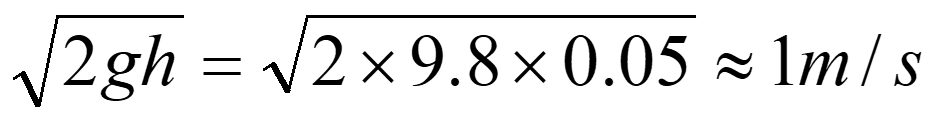
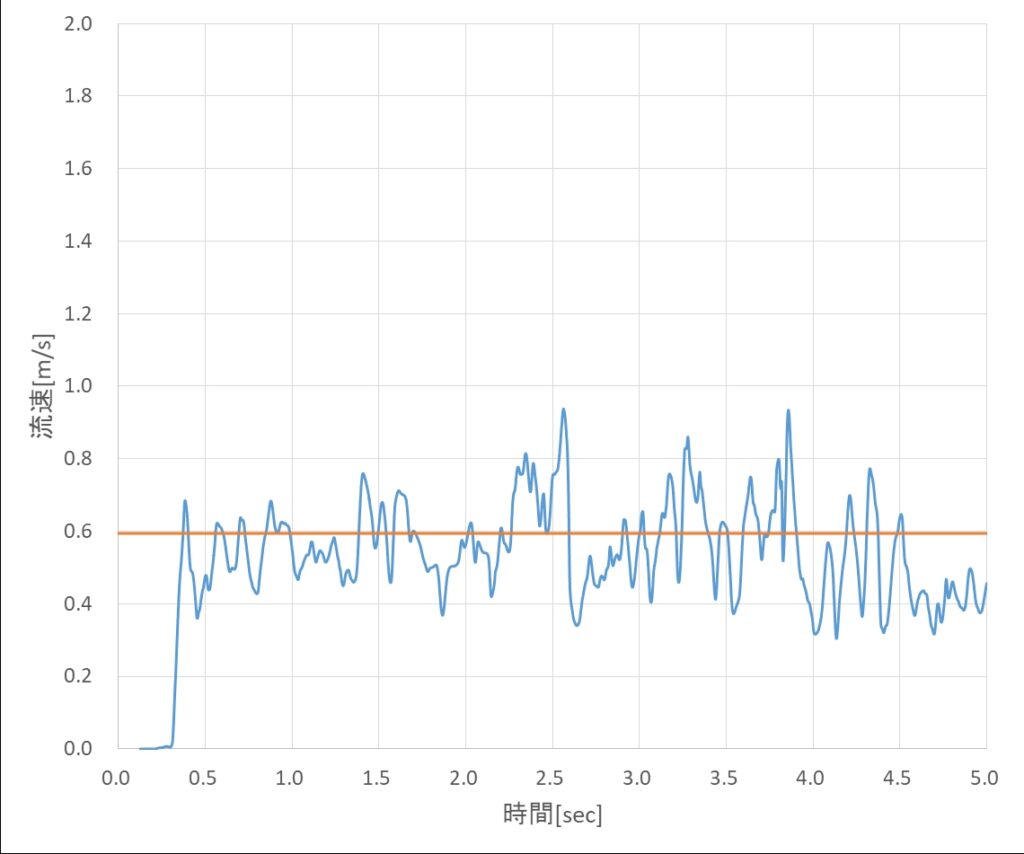
と見積もることができます。実際にはノズル壁面での流速低下があるため、前述のように、0.6×1m/sが、surfaceFieldValue.datから求めた流出速度に近い値となり、図13に示すように、ノズルからの流出流量は、時間に依らず0.6m/sで一定となることがわかります。
次回は、ピタゴラスの盃をOpenFOAMで再現してみます。ピタゴラスの盃とは、盃の中に一定以上の液体が注がれると、サイフォン効果により盃の中の液体が底から流れ出すというもので、ピタゴラスが発明したといわれています。
このページでは、各アプリケーションの操作説明は省略しています。FreeCADの具体的な操作については、いきなりOpenFOAM第5回および第7回、OpenFOAMでの計算実行は第8回、ParaViewの操作については第3回、第4回および第8回を参考にしてみてください。
おことわり
本コンテンツの動作や表示はお使いのバージョンにより異なる場合があります。
本コンテンツの動作ならびに設定項目等に関する個別の情報提供およびサポートはできかねますので、あらかじめご了承ください。
本コンテンツは動作および結果の保証をするものではありません。ご利用に際してはご自身の判断でお使いいただきますよう、お願いいたします。

