いきなりOpenFOAM (54)
二次流れ
解析モデルとメッシュ作成
二次流れは主流と直角な方向に引き起こされる流れで、ダクトの曲がり部分などに発生し、ダストの堆積やダクト内面の浸食の原因となります。
(参考)https://www.jsme.or.jp/jsme-medwiki/09:1009468
二次流れは流体力学において重要な現象ですが、概念だけで現象を理解することは難しいです。そこで、二次流れをOpenFOAMで再現してみます。二次流れだけであれば、曲がりダクト内の単一流体の解析でも確認できますが、今回は、自由表面解析と組み合わせて、河川の二次流れを再現してみます。
始めに、モデルを設計します。図1に示す水路に水が流れる様子を確認することにします。また、流量が100m3/sで水深が10mとなるようにします。この場合、水深は下流の堰高さに依存します。試行錯誤で目標の水深となる堰高さを求めることもできますが、いきなりOpenFOAM第38回で説明した水理学を用いて、必要な堰高さを求めてみます。
まず、限界水深を求めます。限界水深とは堰を越える流れの堰上の水深で下記の式で求められます。
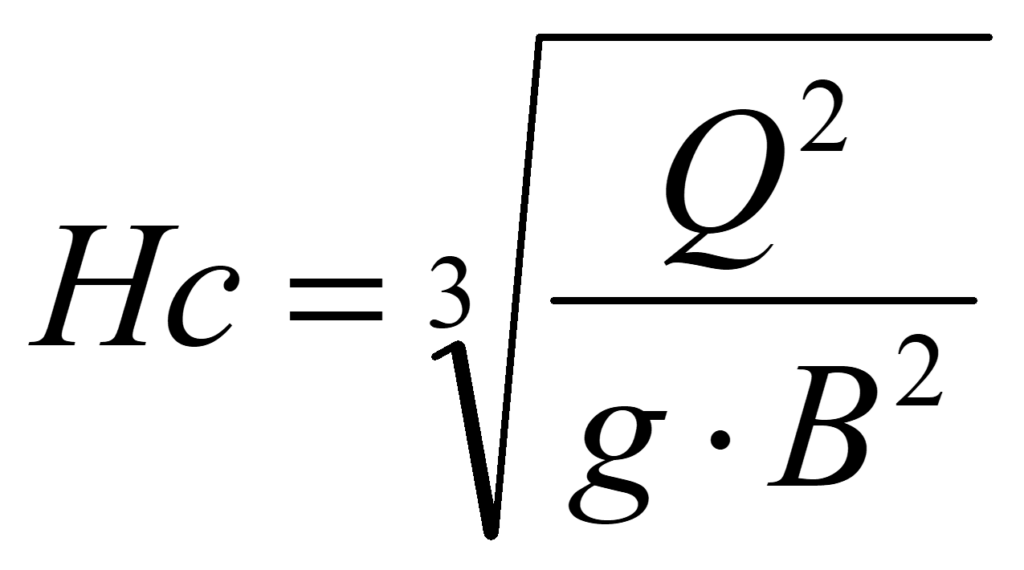
ここで、Qは流量で100m3/s、Bは水路の幅で10m、gは重力加速度で9.8m/s2です。
以上から限界水深Hcは、
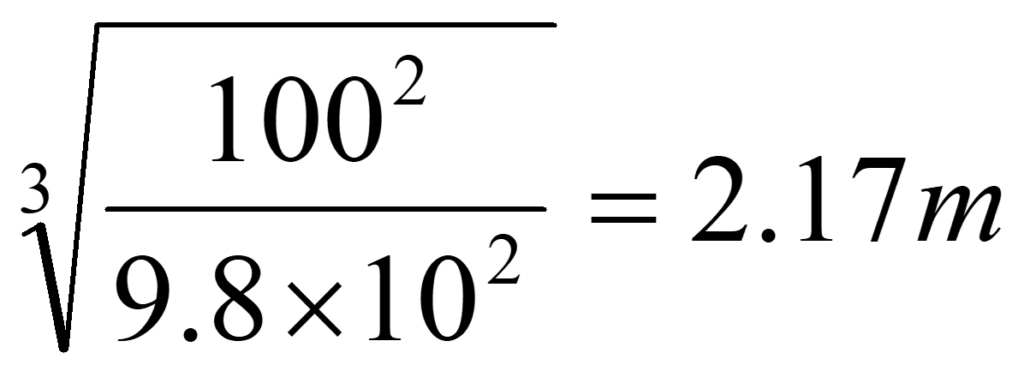
となります。堰高さと限界水深の和が堰上での水面高さとなりますが、いきなりOpenFOAM第38回の水面高さの変化からもわかるように、堰上流の水面高さは堰上の水面高さよりも高くなります。これは、堰上流の流速が堰上の流速よりも小さいため、ベルヌイの定理より水頭が大きくなるためです。今回のケースでこの影響を計算してみます。
堰上流での流速は流量100m3/sと目標の水深10mおよび水路幅10mとから1m/sとなります。一方、堰上での流速は同様にして、100 / (10×2.17) = 4.6m/sとなります。したがって、ベルヌイの定理から堰上流と堰上との水頭差は、(4.62 – 12) / (2×9.8) = 1.03mとなり、この分だけ堰上流側の水面高さが堰上のそれよりも大きくなります。したがって、必要な堰の高さは 10 – 2.17 – 1.03 = 6.8mとなり、下流に高さ6.8mの堰を設ければ、水深が10mとなると考えられます。
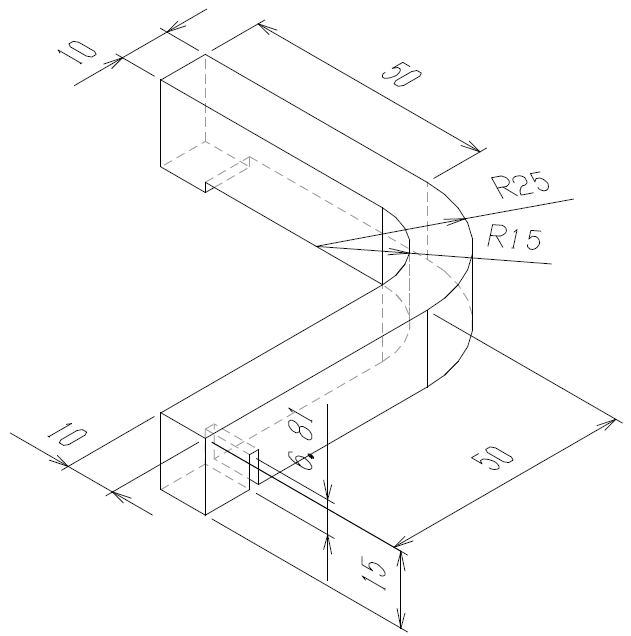
上記の寸法をもとに、図2に示すようにCADで流路を作成します。次いで、面に分割し、図3に示すように、赤色の面は流入口でinlet、青色の面は流出口でoutlet、黄色の面は大気開放でatmosphere、その他の面は壁面でwallsとして、stlファイルを出力します。
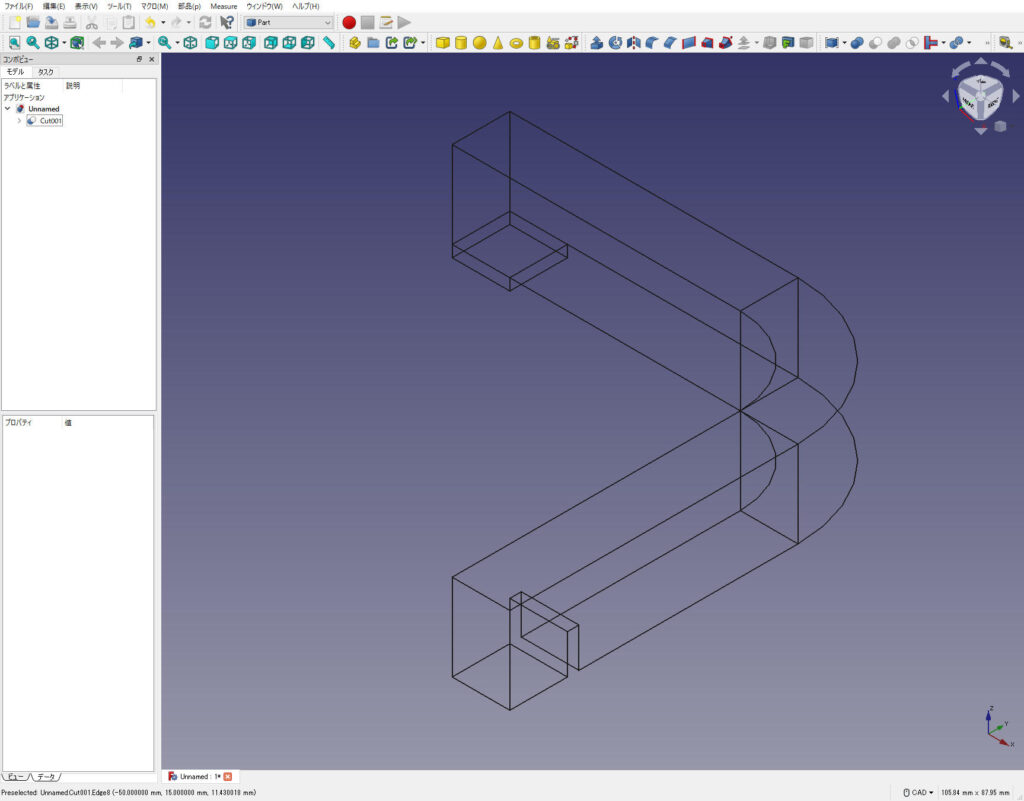
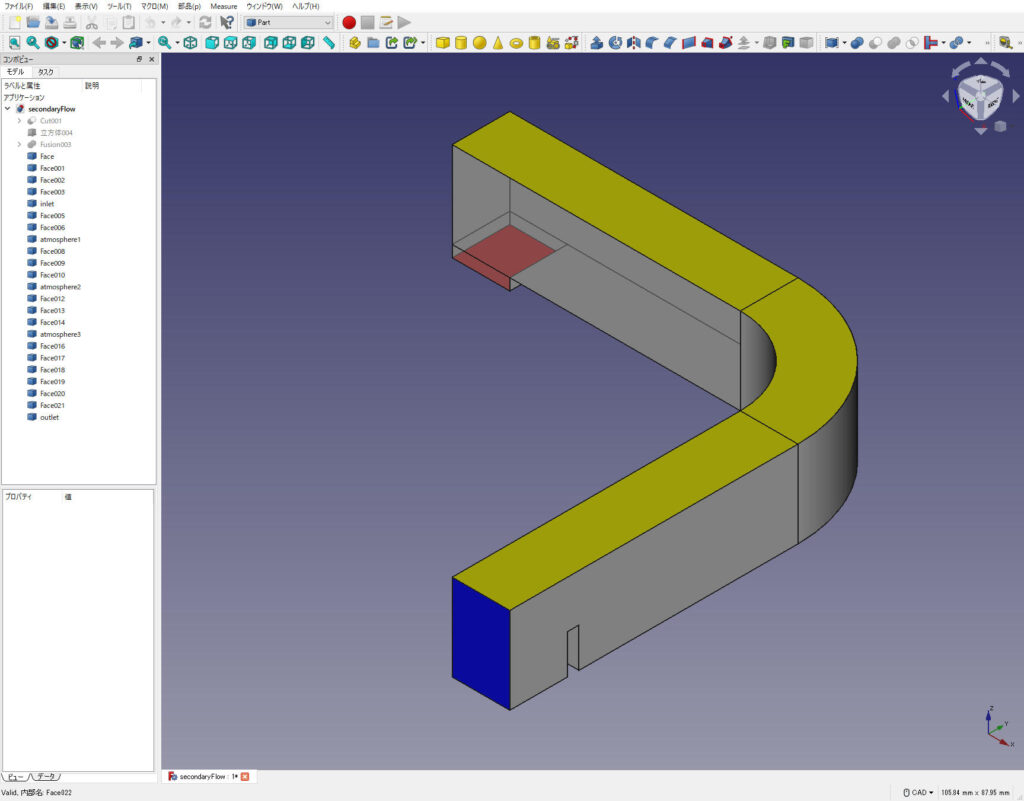
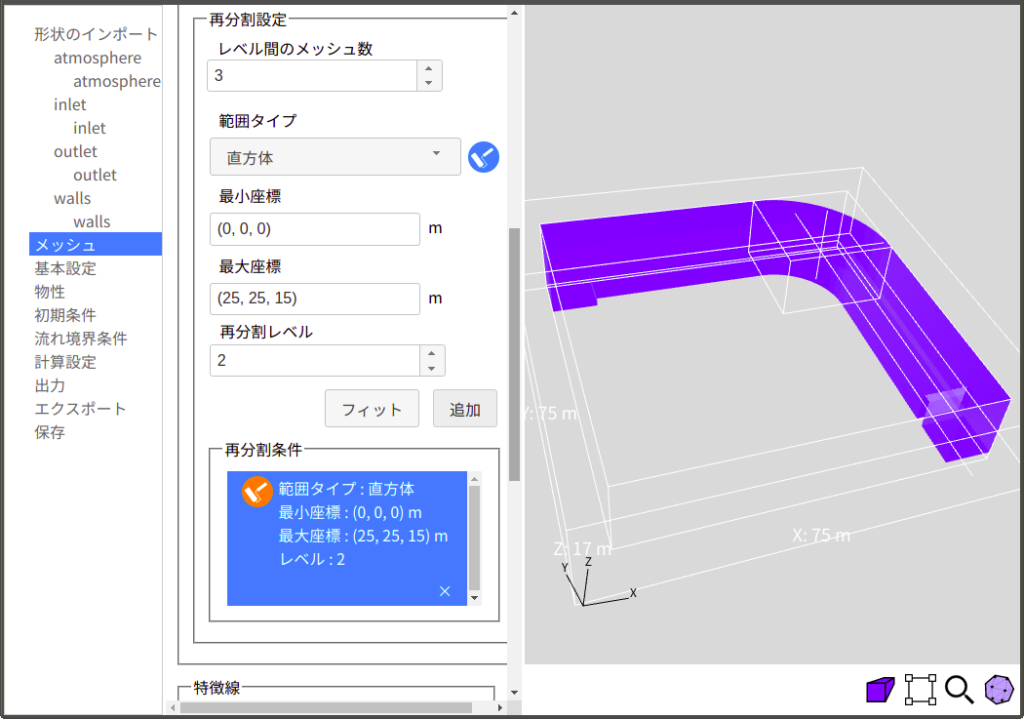
ブラウザでXSimを開き、先ほど出力したstlファイルをインポートします。今回はメートルサイズのモデルのためスケールの変更は不要です(stlファイルは数値のみの情報であり、例えば、図1の10がCADでは10mmを意味していても、XSimでは10mと認識するため)。次に、メッシュ設定では、流路内にメッシュが生成されるように計算領域を (15,15,5)などの流路内の任意の点に変更します。また、図4に示すように、曲がり部分に再分割領域を設定し、領域wallsにデフォルト設定で境界層を設けます。エクスポートで解析ファイルを出力、展開した後、端末からコマンド./Allrun –mでメッシュを生成します。
ファイルの修正
解析は、いきなりOpenFOAM第36回で用いた解析ファイルを流用できます。解析ファイルをフォルダごとコピーして、constantフォルダ内のpolymeshフォルダを生成されたpolymeshフォルダに入れ替えます。次いで、0フォルダ内のUファイルのvolumetricFlowRateを1e2に変更します。このままでも解析は可能ですが、初期条件で水深10mとなるようにsystemフォルダ内にsetFieldsDictファイルを追加すると、モデル内に水が充填されるまでの時間を省くことができます。また、systemフォルダ内のcontrolDictファイルの解析終了時間を流速1m/sでモデル内の水が入れ替わるまでの時間を目安として150秒程度に設定します。詳細はいきなりOpenFOAM第45回と第36回を参照してください。
ファイルを修正・上書き保存したら、端末で、setFields、interFoamの順にコマンドを入力すると、計算が始まります。
結果の可視化
計算が終了したら、paraFoamと入力し、Paraviewを起動して結果を可視化します。図5は150秒後の水面を表示したものです。モデル内の水深は10mと設計通りとなっています。図では水面に流速をコンター表示しています。図を見ると、堰より上流では流速が1m/s程度と常流に、また堰より下流では流速が増加し、射流となっていることがわかります。
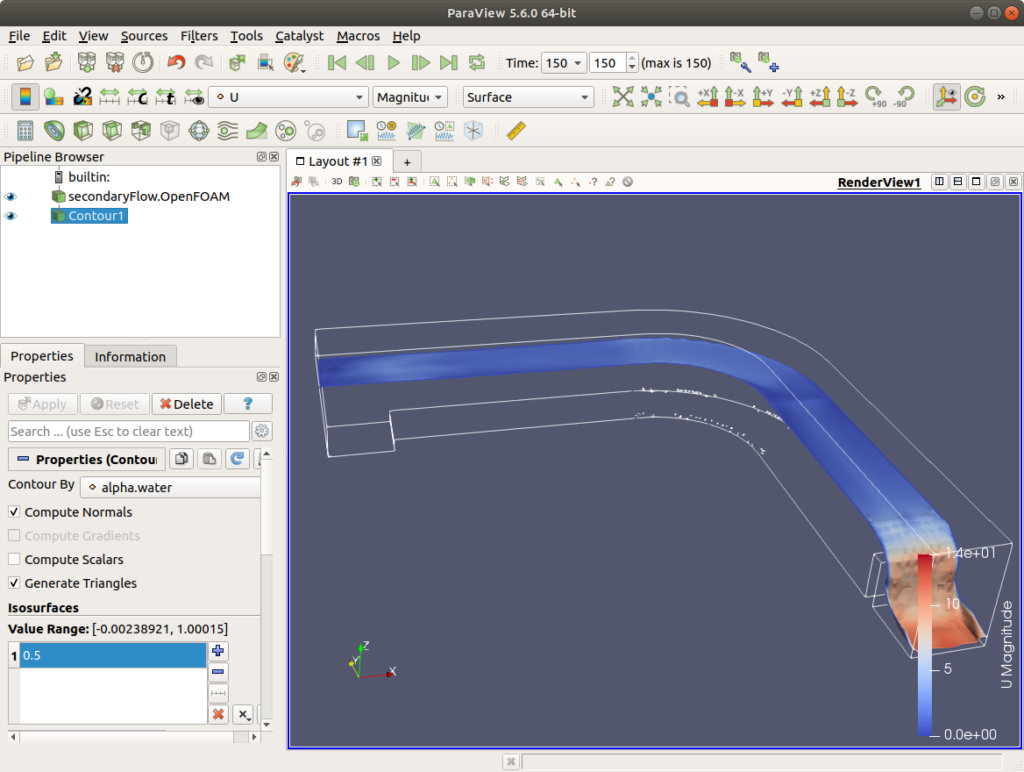
図6は水深5mでの流速分布を示しています。図を見ると、曲がり部分に入る手前で、外側に流速の小さい領域が、また、内側に流速の大きい領域が見られます。また、曲がり部分と曲がり部分を通過後では、逆に外側に流速の大きい領域が見られます。断面を変更して、流速分布や静圧分布を見ると、曲がり部分で発生している現象の理解に役立ちます。
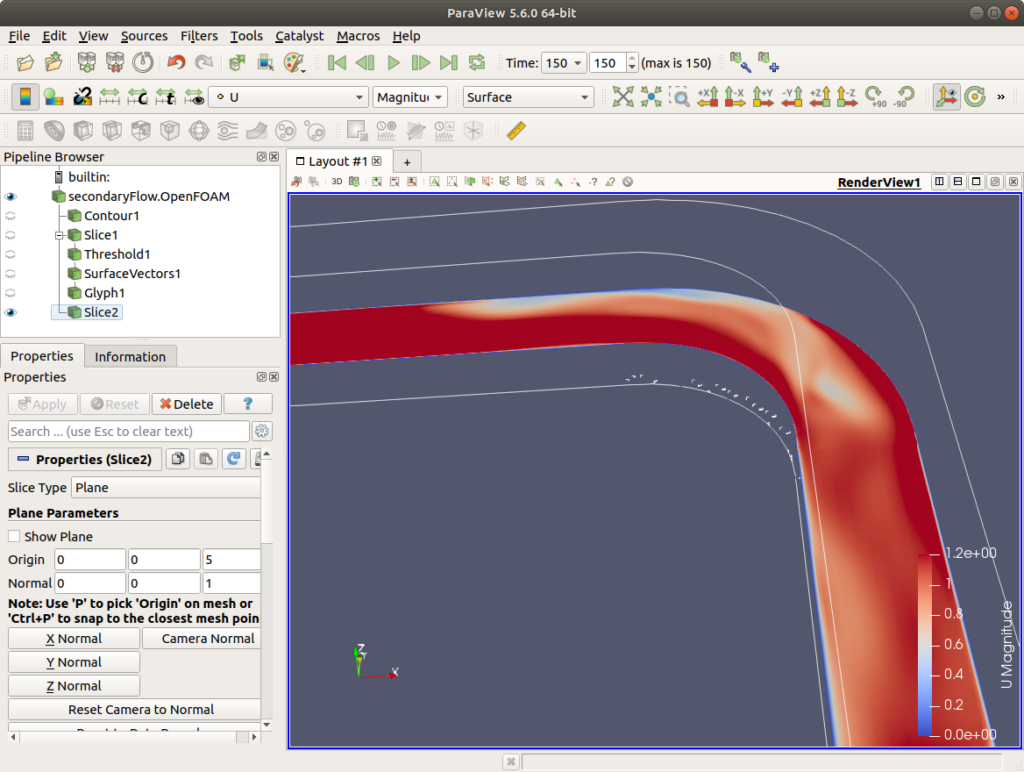
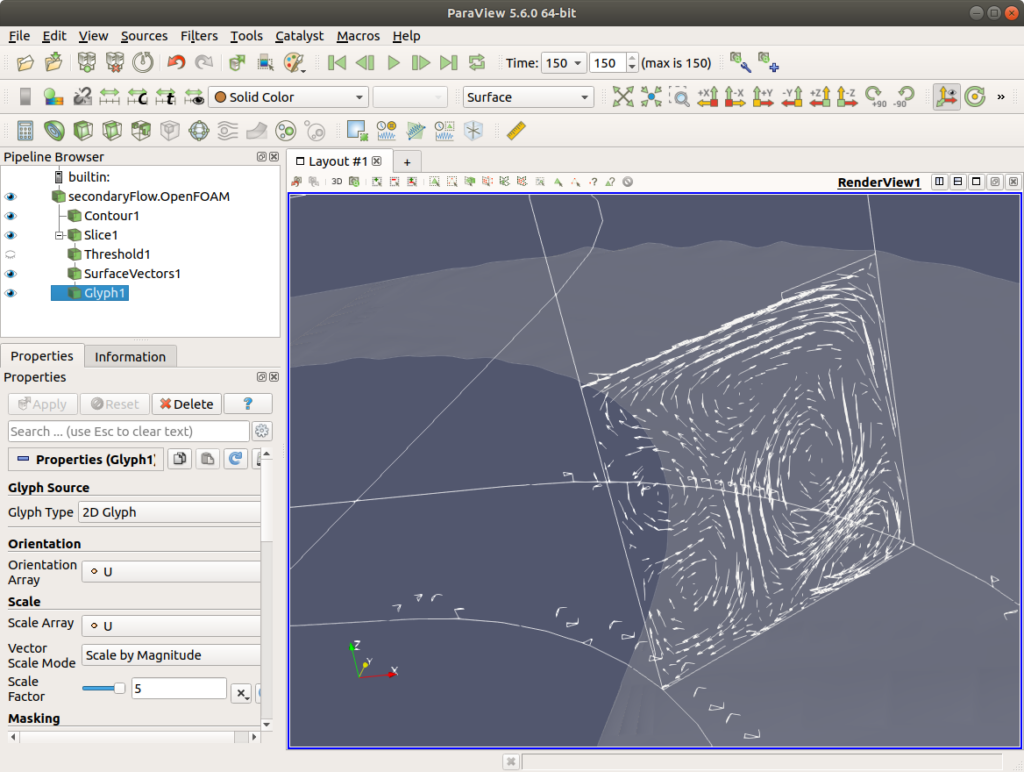
曲がり部分に上から見て45度の断面を設定して流速をベクトル表示すると、二次流れを観察できますが、そのまま流速ベクトルを表示しても、主流の流速が大きいため、二次流れ成分が見えにくくなります。そこで、Filters→SufaceVectorsとして、断面に投影された流速成分を求めてからGlyphで流速ベクトルを表示すると、図7に示すように、二次流れを表示できます。
図8は流線を表示しています。図を見ると、流線は二次流れにより水深の深い部分から浅い部分へ向かう流れと深い部分から浅い部分に向かう流れなどに分かれることがわかります。

これまでは、メッシュが静止した状態での解析でしたが、メッシュが移動できれば、揺動する容器内の液体の挙動などを解析できます。次回からメッシュ移動機能について説明します。
このページでは、各アプリケーションの操作説明は省略しています。FreeCADの具体的な操作については、いきなりOpenFOAM第5回および第7回、OpenFOAMでの計算実行は第8回、ParaViewの操作については第3回、第4回および第8回を参考にしてみてください。
おことわり
本コンテンツの動作や表示はお使いのバージョンにより異なる場合があります。
本コンテンツの動作ならびに設定項目等に関する個別の情報提供およびサポートはできかねますので、あらかじめご了承ください。
本コンテンツは動作および結果の保証をするものではありません。ご利用に際してはご自身の判断でお使いいただきますよう、お願いいたします。

