いきなりOpenFOAM (60)
1自由度系振動モデル(その1)
1自由度系振動モデルとは
前回のスロッシング現象の解析結果を見ると、液面は周期的に変動する振動現象とみなせます。振動現象を理解するには、振動工学の初歩である1自由度系振動モデルについて理解する必要があります。1自由度系振動モデルは、図1に示すように、質量mとバネkとダンパcとからなります。1自由度のため、質量mはy方向のみに運動します(自由度とは移動・回転できる方向で、完全に自由な物体は、x軸、y軸、z軸に沿った方向とx軸、y軸、z軸周り回転の計6つの自由度を有します)。
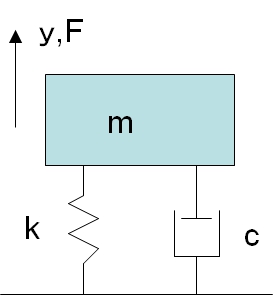
図1の質量mの運動方程式は、重力を無視すると下記のようになります。
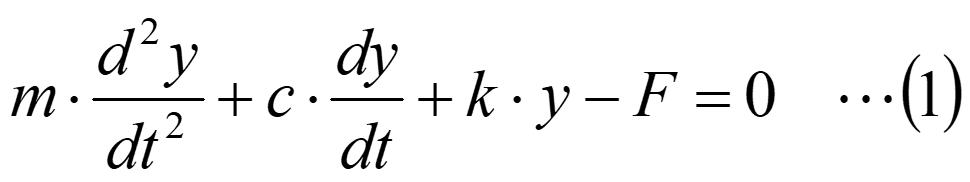
ここで、mは質量[kg]、kはバネ定数[N/m]、cは減衰係数[Ns/m]でFは質量mに加わる外力[N]です。
地震の場合は、質量mに地震の加速度α[m/s2]が加わるため、下記の式となりますが、F=m×αとして外力とみなすと、(1)式と同じです。
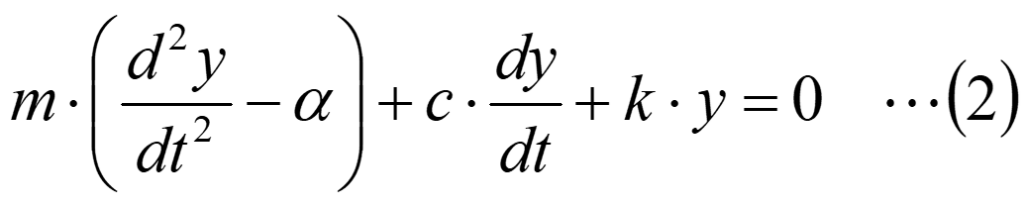
さて、(1)式は解析的に解くことが可能で、yは下記のように表されます。
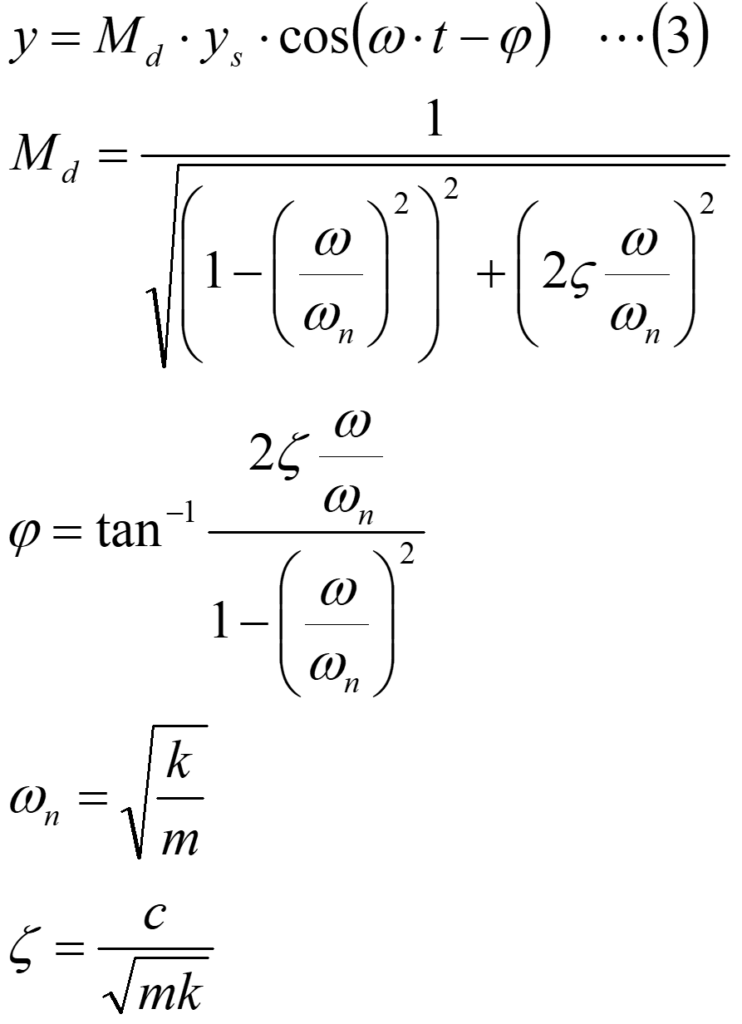
ここで、ysは外力の振幅が静的に作用した場合の静的変位[m]、ωは外力の角振動数[rad/s]です。
Pythonを用いた数値解法
振動工学では、(1)式の運動方程式から(3)式で表される変位の時間変化を導出し、振動現象を説明します。ただし、(3)式はかなり複雑で、また、概念的な説明では、わかりづらいため、ここでは数値的に(1)式を解くことで、振動現象を可視化して理解することにします。微分方程式の数値解法はMATLABなどのエンジニアリングソフトを用いれば容易に行えます。今回は、Pythonを用いて数値的に解く方法を説明します。現象をモデル化して、数値的に可視化することで理解する手法は、モデルベースデザインと呼ばれ、コンピュータの発達により近年急速に普及しています。
なお、(3)式は複雑な式ですが、振幅倍率と呼ばれるMdが求められれば、ある外力の周波数に対して振動の大きさを予測できるため、実用には十分と言えます。振幅倍率Mdは、質量m、バネ定数k、減衰係数cから計算できますが、実験から求めることも可能です。したがって、スロッシング現象における振幅倍率をOpenFOAMでの計算結果から求められれば、スロッシングを考慮した設計に役立てることができます。
エンジニアリングソフトでも、2階微分方程式を直接解くことはできないため、(1)式を下記のように、1階の連立微分方程式に置き換えます。
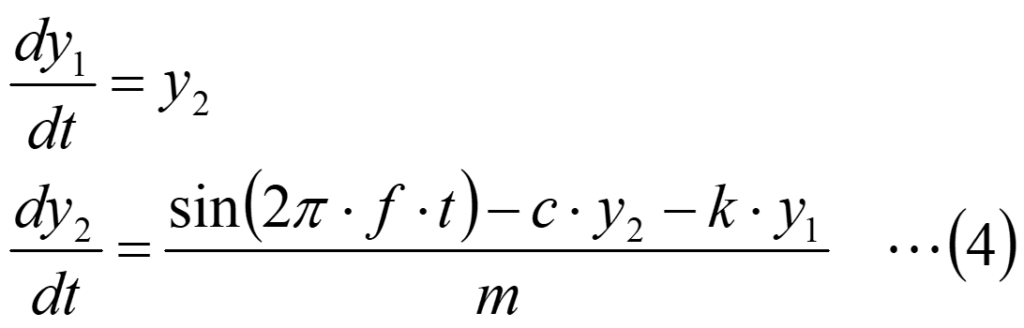
ここで、外力Fとして、sin(2π・f・t) という振動周波数f[Hz]の強制振動を与えます。
(4)式を数値的に解いて、結果を図示するには、図2に示すコードを用います。図2のコードの中心となるのは、odeintという関数で、odeint(微分方程式、初期値、時間変数、係数)の形で、微分方程式の数値解法結果を返します。odeintを用いるには、numpyとscipyというモジュールが必要となるため、コードの先頭で、import numpyとfrom scipy.integrate import odeintとして呼び出しています。同様に、グラフ表示させるために、from matplotlib import pyplotとしてグラフ作成モジュールを呼び出しています。なお、あらかじめ、numpy、scipy、matplotlibのインストールが必要ですが、anacondaでは、Python本体のほか、先ほどのモジュール類や統合開発環境も一体でインストールできます。
図2のコードではdydtとして、(4)式を無名関数で定義しています。また、(4)式の係数は(m,c,k,f)として、タプルを用いて定義しています。y0は初期値で、(変位初期値、速度初期値)の順です。また、Nは分割数、tは計算時間で、図2では、0から50秒未満まで、50/10000=5ms刻みで計算させます。解法結果は、変位配列、速度配列の行列で表され、ここでは変位を求めたいので、y=sol[:,0]として、変位yを取り出しています。図2のコードを動作させると、図3のような結果が得られます。
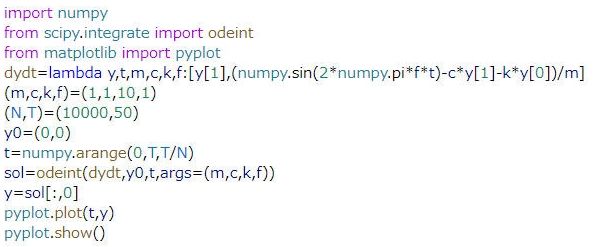
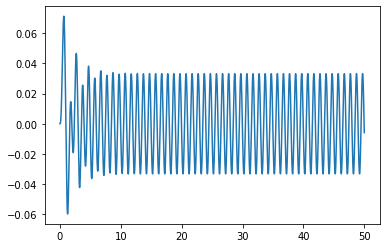
図3でも結果としては十分ですが、設定した係数や縦軸、横軸の説明があったほうが分かりやすくなります。図4は図2のコードにグラフ表示の設定を追加したものです。図4のコードを動作させると、図5に示すような結果が得られます。

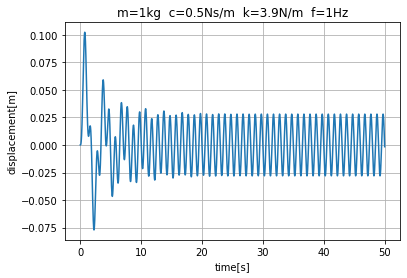
また、数値解法結果をエクセルで処理したい場合は、結果をcsvファイルとして保存できます。図6のコードは、グラフ表示の代わりに、結果をcsvファイルとして保存するようにしたコードです。図6のコードを動作させると、1列目に時間、2列目に変位の計算結果が並んだcsvファイルがresult2.csvというファイル名で出力されます。

次回は、(1)式の係数を変更して計算した結果をもとに、強制振動の特徴を説明します。また、振幅の周波数特性を求めてみます。
おことわり
本コンテンツの動作や表示はお使いのバージョンにより異なる場合があります。
本コンテンツの動作ならびに設定項目等に関する個別の情報提供およびサポートはできかねますので、あらかじめご了承ください。
本コンテンツは動作および結果の保証をするものではありません。ご利用に際してはご自身の判断でお使いいただきますよう、お願いいたします。

