いきなりOpenFOAM (61)

1自由度系振動モデル（その2）

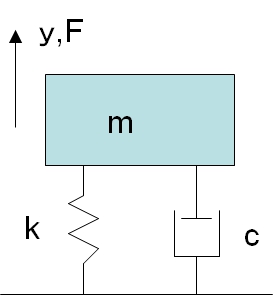
　今回は、加振周波数を変えて振動特性を計算してみます。基本的には、いきなりOpenFOAM第60回で説明したコードで計算できますが、地震を想定して、運動方程式を下記のように変更して解いてみます。

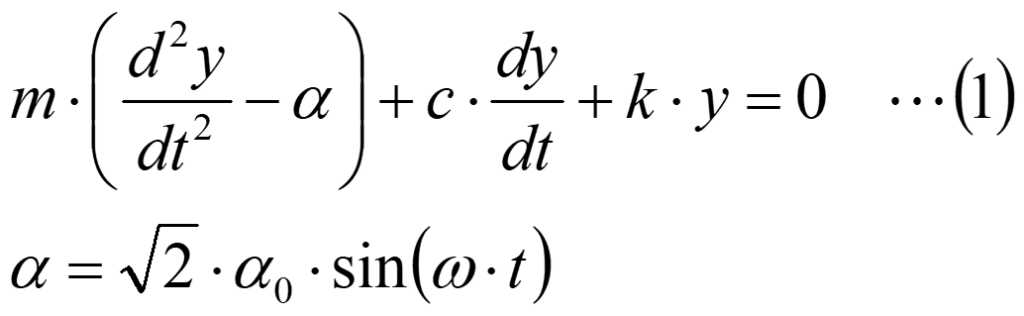
あわせて、1Hzで共振するように質量ｍとバネ定数ｋを設定します。固有角振動数は

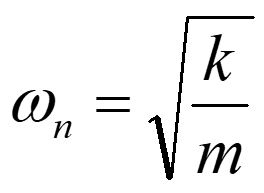
となるので、m=1kgとk=39.5N/mの組み合わせで、角振動数が2π rad/s、すなわち周波数が1Hzとなります。以上を設定すると、図2に示すコードで、任意の周波数、任意の加速度での振動特性が得られます。

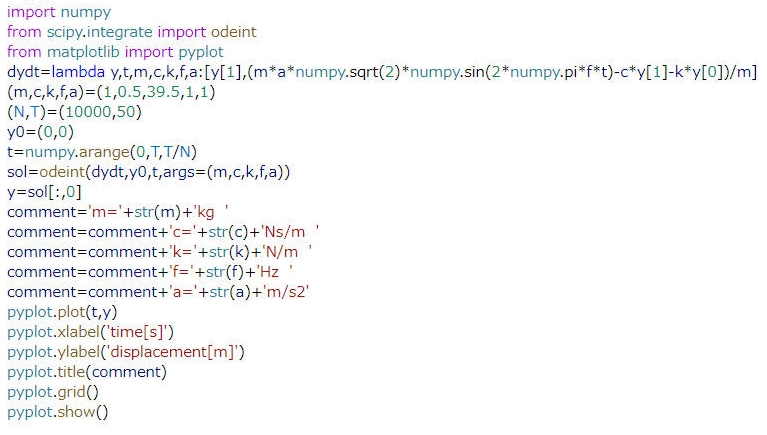
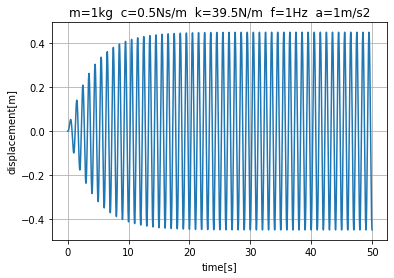
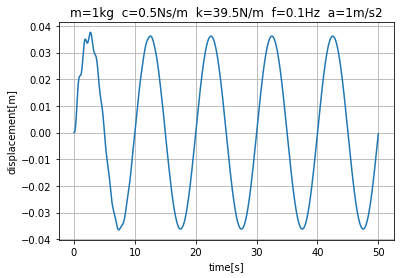
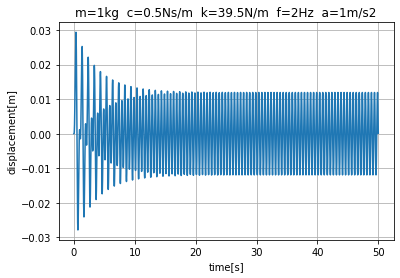
　図2に示すコードで、加振周波数を1Hzに設定すると、図3に示す結果が得られます。時間の経過とともに振幅が増大し、飽和する様子が見られます。先述のように、固有周波数は1Hzで加振周波数と一致し、共振状態と呼ばれます。共振状態では、加振と同時に振幅は増大し、減衰係数に応じた値で飽和します。図4は加振周波数を0.1Hzで同様にして計算した結果です。図3と比較すると、振幅は1/10以下となることがわかります。また、図4は加振周波数を2Hzにして計算した結果です。同様に、振幅は図3の1/40以下となることがわかります。このように、振動が問題となる系では共振状態を避ける、つまり、固有周波数を外乱の周波数と一致させないことがポイントとなります。

　加振周波数を変化させて、(1)式の運動方程式を数値的に解くと、振幅の周波数特性が得られます。図6は、加振周波数を0.1～2Hzまで0.1Hz刻みで変化させながら振幅を求めるコードです。図2のコードにForループで加振周波数ｆを変化させる部分を追加し、変位の時間波形の後ろ10秒分から最大値を求めて、定常時の振幅としています（このあたりの処理は暫定の方法です。実際はFFT処理などのさらに良い方法があります）。
　図6のコードを動作させると、図7に示す振幅の周波数特性が得られます。図を見ると、固有周波数1Hzを中心に山を描き、固有周波数との差が0.1Hzでも振幅は大きく低下することがわかります。

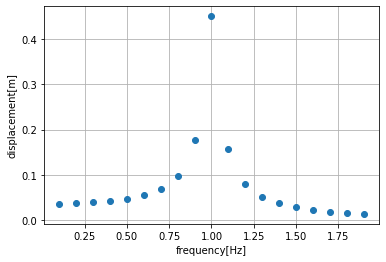
　振動を問題とする場合、図7に示すような周波数特性が得られれば、問題を回避あるいは解決する際の有力な指針となります。今回の場合は、コードによるシミュレーションのため、短時間で結果が得られましたが、振動の実験やCFDによりスロッシング現象を測定する場合は、繰り返しとなるため、長い時間を要します。そこで、いきなりOpenFOAM第60回で説明した解析解の振幅倍率Mdを実験的に求められれば、加振周波数の影響を簡単に求めることができます。インパルス応答と呼ばれる手法がそれで、次回は、インパルス応答を用いて、振幅の周波数特性を求めてみます。

おことわり
　本コンテンツの動作や表示はお使いのバージョンにより異なる場合があります。
　本コンテンツの動作ならびに設定項目等に関する個別の情報提供およびサポートはできかねますので、あらかじめご了承ください。
　本コンテンツは動作および結果の保証をするものではありません。ご利用に際してはご自身の判断でお使いいただきますよう、お願いいたします。