いきなりOpenFOAM (62)
1自由度系振動モデル(その3)
インパルス応答
前回は、各種の加振周波数で振動系を表す運動方程式を解くことにより、振動系の周波数特性が得られることを説明しました。ただし、この方法では、周波数ごとに振動測定を行う必要があり、手間と時間がかかります。これを一回の実験で周波数特性を得る方法がインパルス応答などと呼ばれています。インパルス応答では、ハンマーで叩くなどで瞬間的な加速度変化を与えて、振動波形を測定し、振幅倍率を求めます。ここでは、インパルス応答の手順について説明します。インパルス応答の詳細については、参考文献などを参照してください。
参考文献:JSMEテキストシリーズ振動学、日本機械学会
数値シミュレーションにおけるインパルス応答の測定
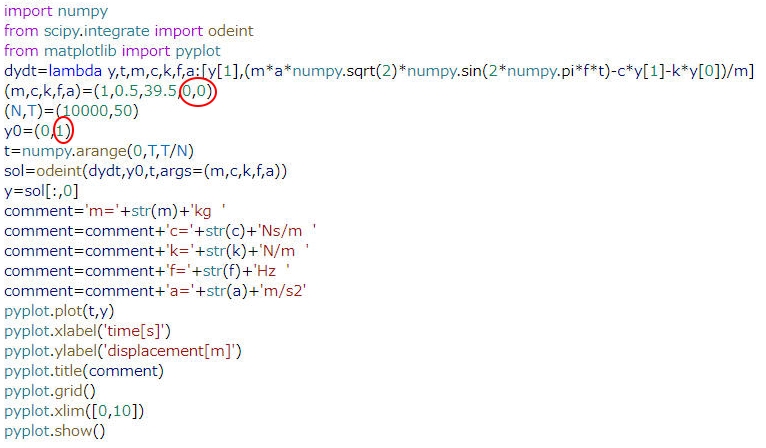
数値シミュレーションでは、瞬間的な加速度を与えることができないため、初期条件として適当な速度を与えて、外力を0として解析を行います。加速度は速度の微分のため、速度に0以外の初期条件を設定すると、計算開始時に初期速度/分割時間という非常に大きな加速度が発生します。これを利用してインパルス応答を測定してみます。具体的には、図1に示すように、外力を0にして初期条件y0の速度をここでは1m/sに設定しています。
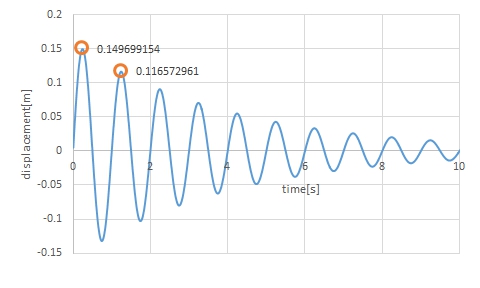
図1のコードを動作させると、図2に示すように、徐々に減衰する振動波形が得られます。これがインパルス応答です。
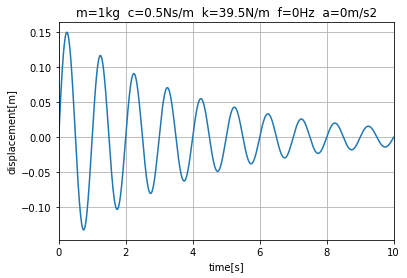
次に、インパルス応答波形から、下記の振幅倍率Mdを求めます。振幅倍率については、いきなりOpenFOAM第60回を参照してください。
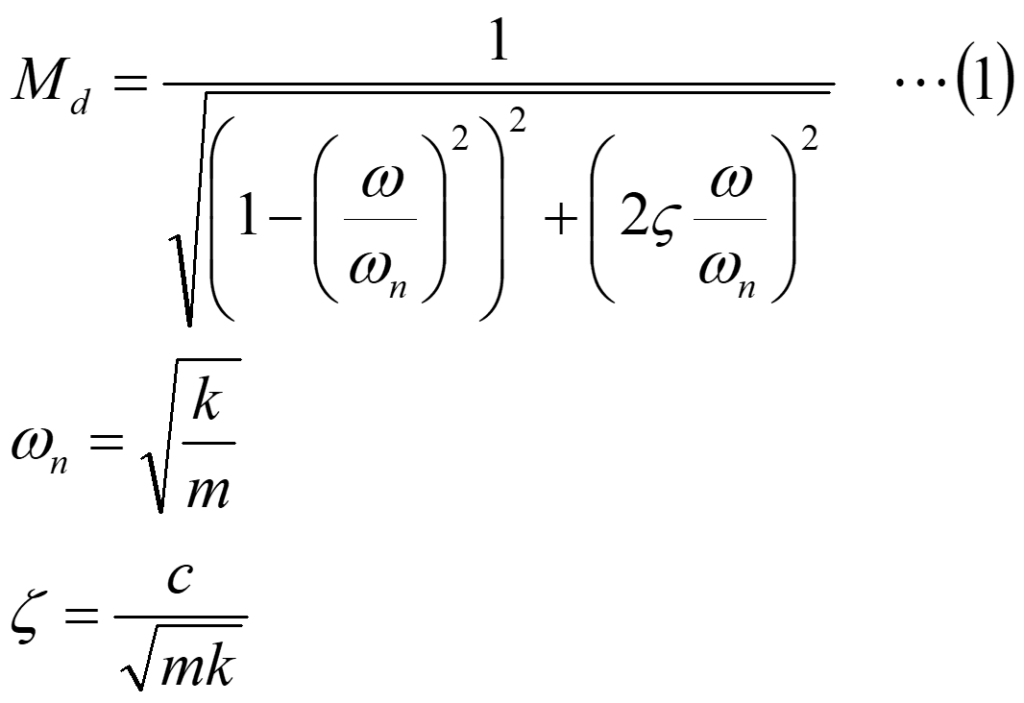
具体的には、インパルス応答波形の隣り合った極大値同士の時間間隔を測定し、2πを時間間隔で割ると、振動系の共振角周波数ωnが求まります。また、隣り合った極大値の比の自然対数を求めて、2πで割ると、減衰比ζが求まります。ここでは、インパルス応答波形をcsvファイルとして出力して、表計算ソフトなどで手作業で計算を行っていますが、Pythonで処理を行わせてもかまいません。csvファイルへの出力については、いきなりOpenFOAM第60回を参照してください。
図3はインパルス応答波形のcsvファイルをグラフ化したものです。例えば、橙色の〇の箇所の極大値の時間差は1秒で、共振周波数は1Hzとなり、いきなりOpenFOAM第61回で設定したように、図1のコードの固有周波数1Hzと一致します。共振角周波数ωnはラジアン単位のため、共振周波数に2πを掛けた値となります。
次に、減衰比ζ を求めます。減衰比ζ は隣り合った極大値の比の自然対数を求めて、2πで割った値になります。例えば、図3では、
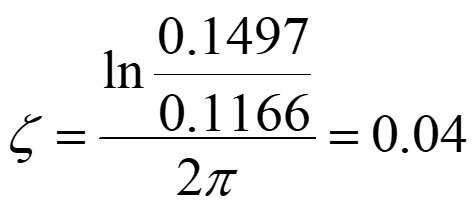
となります。
以上を(1)式に代入して、外力の角周波数ωに対する振幅倍率Mdを求めると、図4に示す結果が得られます。図を見ると、外力の周波数が1Hzで振幅倍率が最大となり、共振状態となることがわかります。
このままでは、使いにくいので、任意の周波数の外力を加えた場合の振幅を求めて、その周波数での振幅倍率との比を掛けると、図5に示すように変位の周波数応答が得られます。今回は、いきなりOpenFOAM第61回で説明したように、加速度は実効値1m/s2を設定しているので、任意の加速度での変位は図5の値と加速度との積となります。図5の橙色の〇は、いきなりOpenFOAM第61回での周波数を変えた場合の振幅の計算結果です。ここからも、インパルス応答波形から振幅の周波数特性を正しく求められることがわかります。
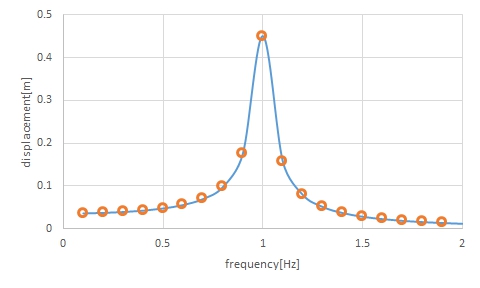
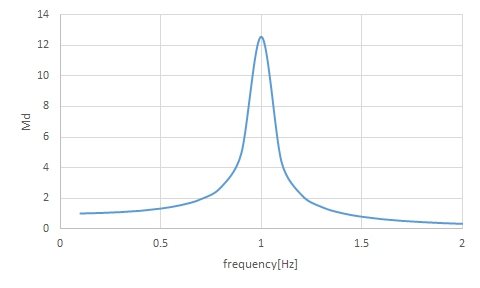
図6は以上の手順をまとめたものです。振動問題に関しては、周波数特性を求めることが、アプローチの第一となり、インパルス応答は比較的手軽に行える手法のため、広く普及しています。

スロッシング現象は、厳密には一自由度系の振動モデルとして扱えませんが、今回の手法を使って、その傾向を探ることが可能です。次回は、いきなりOpenFOAM第59回のスロッシング解析の例で、インパルス応答を求めて、スロッシング高さの周波数特性を求めてみます。
おことわり
本コンテンツの動作や表示はお使いのバージョンにより異なる場合があります。
本コンテンツの動作ならびに設定項目等に関する個別の情報提供およびサポートはできかねますので、あらかじめご了承ください。
本コンテンツは動作および結果の保証をするものではありません。ご利用に際してはご自身の判断でお使いいただきますよう、お願いいたします。

