いきなりOpenFOAM (83):竹とんぼの飛行解析(その2)
解析モデル
前回は、竹とんぼの運動方程式について説明しました。運動方程式の中には、推進力と負荷トルク、流体抵抗力のそれぞれの係数が含まれていて、これらの係数は風洞実験で求める必要があります。今回は、OpenFOAMで数値風洞実験を行い、これらの係数を求めてみます。
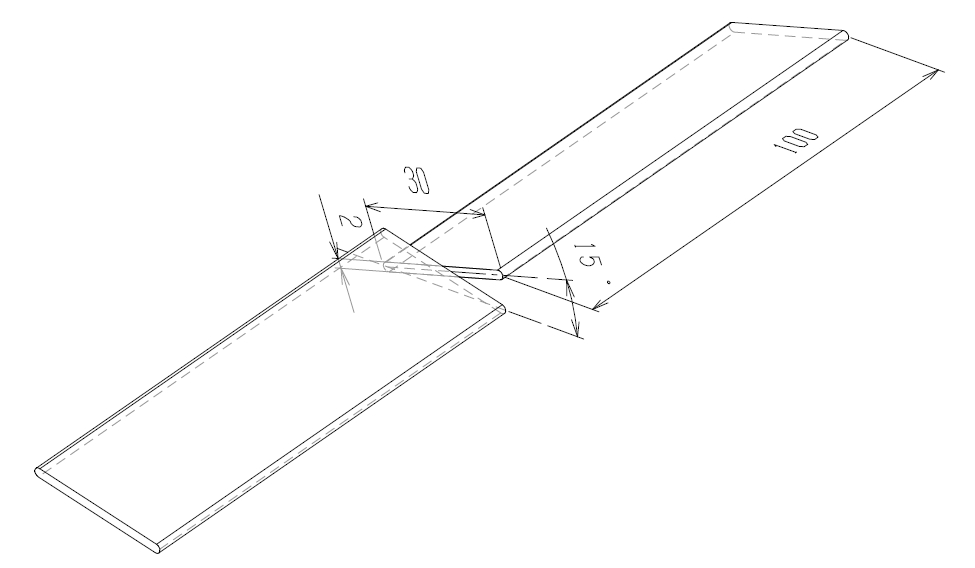
始めに、竹とんぼのモデルを作成します。図1に示すように、水平に対して15度傾いた2枚の平板を組合せて竹とんぼとします。実際の竹とんぼでは姿勢が安定するように軸がありますが、今回は、回転軸が固定された状態で解析を行うため、軸は省略します。
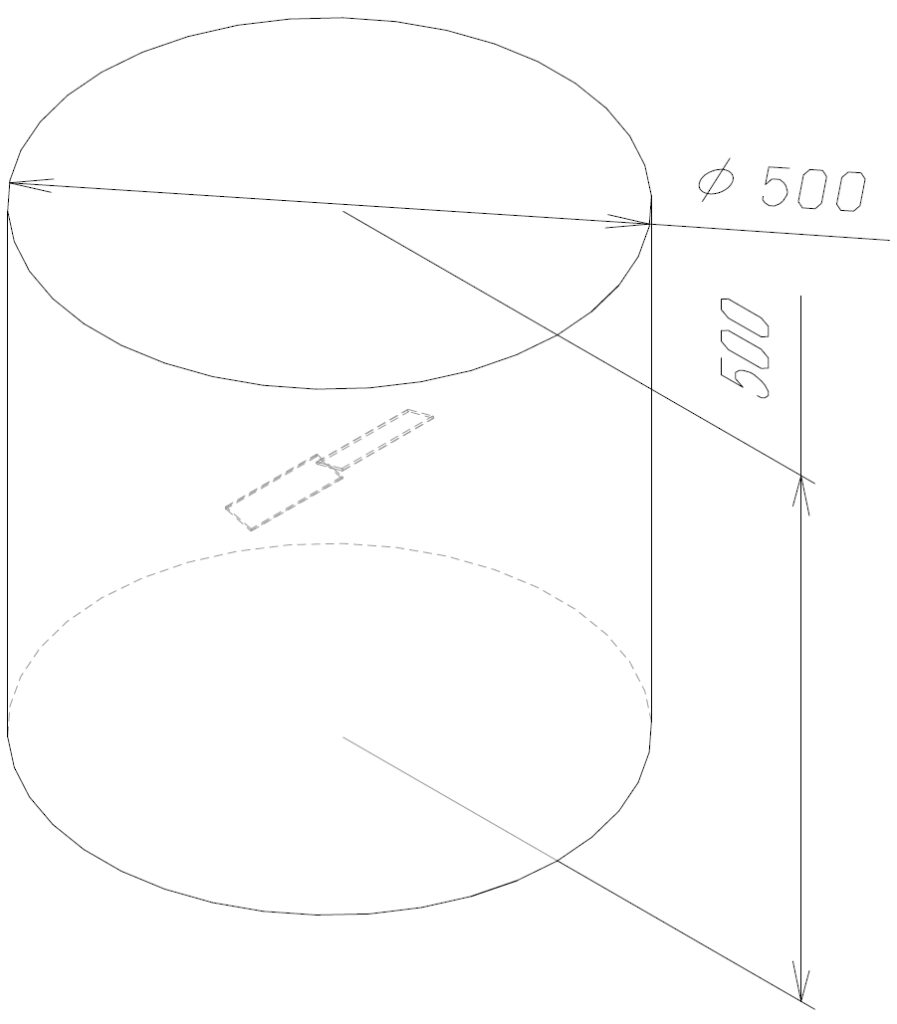
次に、図2に示すように、竹とんぼを円筒空間で囲み、解析モデルとします。円筒空間は境界条件の影響を除くため、竹とんぼに対して十分に大きくする必要がありますが、今回は計算サンプルという目的で、メッシュサイズが大きくならないように、竹とんぼの直径の5倍としています。
解析は、竹とんぼの推進力と負荷トルクを求めるために、静止した空間内で竹とんぼを回転させ、竹とんぼに加わる力とトルクを求めることと、竹とんぼが上昇する際の流体抵抗力を求めるために、円筒内を上から下に向かう気流中で竹とんぼに加わる力を求めることの二種類を行います。
解析モデルをstlファイルに出力する際に、今回は円筒天面をinlet、円筒底面をoutlet、円筒側面をside、竹とんぼをbladeという名称にしました。
メッシュ作成と条件設定
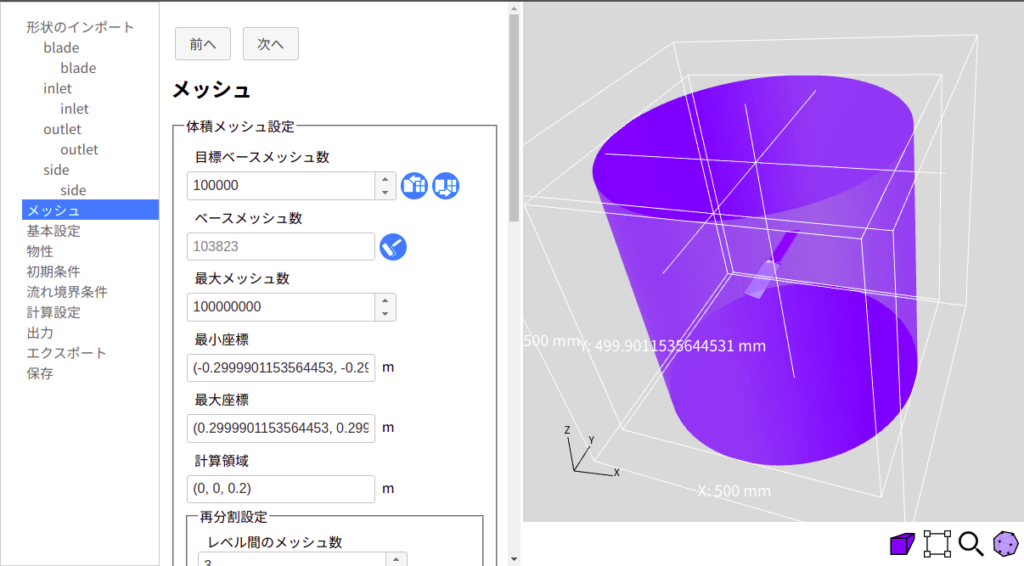
次に、ブラウザでXSimサイトに接続し、出力したstlファイルのインポートとスケールの変更を行います。メッシュ設定では、図3に示すように、目標ベースメッシュ数をデフォルトの10倍に設定します。また、計算領域を指定する座標が回転領域内に含まれないように、デフォルトの値から変更します。
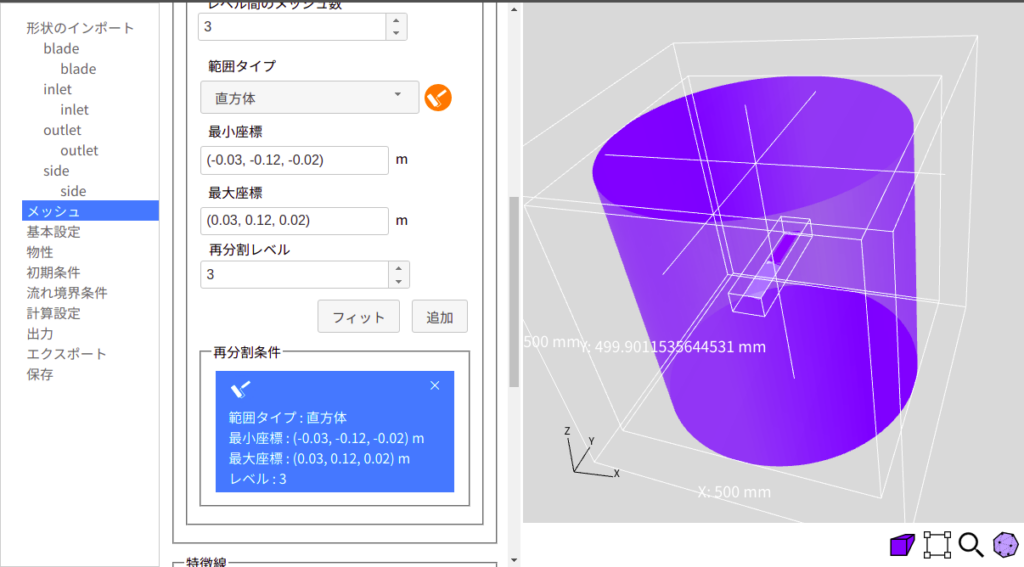
次に、図4に示すように、竹とんぼを囲むように、直方体形状で再分割領域を設定します。また、竹トンボの表面bladeに、デフォルトでレイヤを設定します。
次に、基本設定では、「回転領域」にチェックを入れます。また、「定常解析」を選択します。物性設定では、物性として「Air」を選択します。初期条件では、速度を0に設定します。また、流れ境界条件では、bladeに静止壁を、inlet、outlet、sideには、全圧0を設定します。
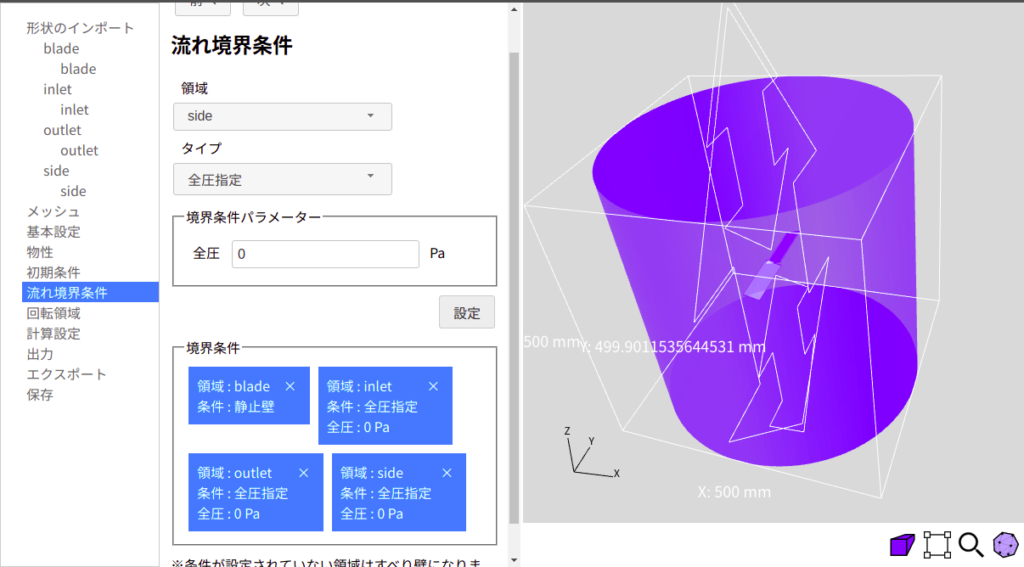
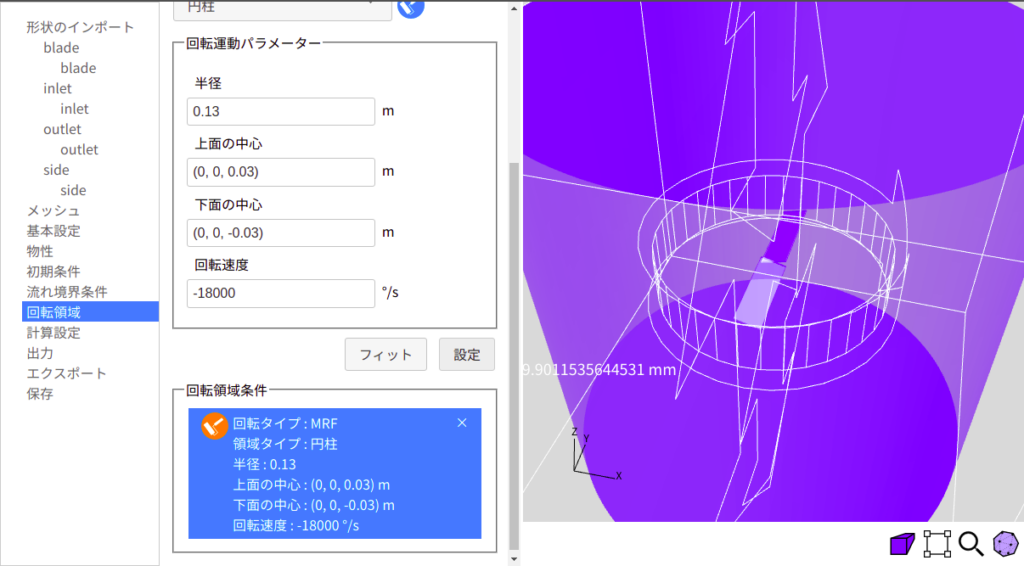
次に、回転領域では、図6に示すように、領域タイプとして円柱を選択し、竹とんぼ周りに円柱状の領域を設定します。回転速度は、上から見てCW方向に3000r/minとして、-18000°/sとします。詳細はいきなりOpenFOAM第69回を参照してください。
次に、計算設定では、緩和係数をデフォルトよりも小さな値に設定します。今回は、速度、乱流エネルギー、乱流散逸率を0.7から0.5に、圧力を0.3から0.2に変更します。詳しくは、いきなりOpenFOAM第25回を参照してください。
出力設定などを行い、エクスポートで解析ファイルを出力します。
竹とんぼに加わる力とトルクを求めるために、物体に働く力とモーメントを求める関数を設定します。XSimから出力された解析ファイルを展開し、Systemフォルダ内に、いきなりOpenFOAM第78回ドローンのプロペラ周りの流れで説明したforcesファイルをコピーペーストします。次に、エディタでforcesファイル内のpatchesを竹とんぼの領域bladeに変更します。また、同様にエディタで、controlDictファイルのfunctionsに、#include “forces”;を追加します。詳細は、いきなりOpenFOAM第78回を参照してください。
ファイルの追加・修正が完了したら、端末から./Allrun –mでメッシュ生成、simpleFoamで計算を実行します。なお、流体抵抗力を求める解析ファイルを次に作成するため、XSimはそのままにしておきます。
結果の可視化(推進力と負荷トルク)
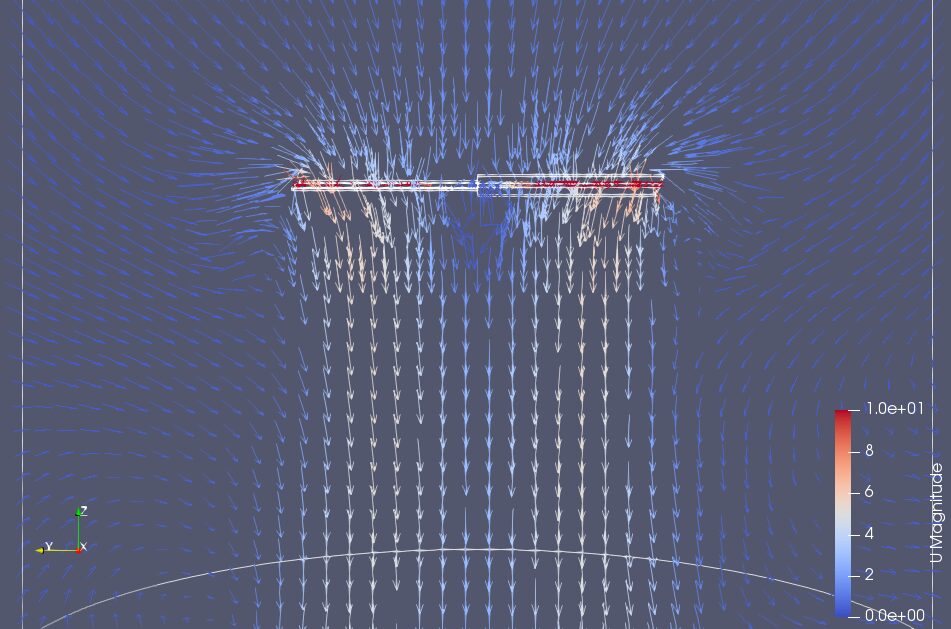
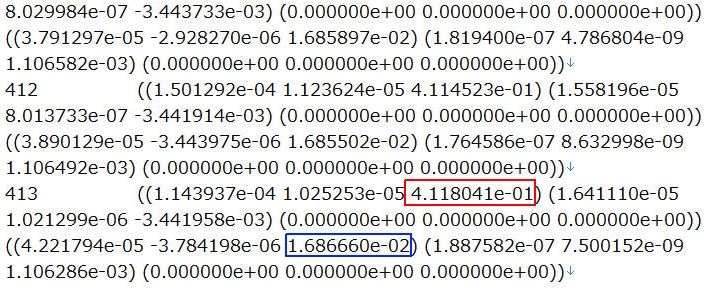
図8に縦断面流速分布を示します。図を見ると、回転する竹とんぼに吸い込まれた気流が下に吹き付けられる様子がわかります。推進力と負荷トルクは、postProcessingフォルダ内にforces.datファイルとして出力されます。forces.datファイルの図9に示す赤い枠で囲まれた数値が推進力で、青い枠で囲まれた数値が負荷トルクです。
流体抵抗力の算出
次に、流体抵抗力を求めます。図9に示すように、流れ境界条件で、inletに下向きに1m/sを設定し、outletには自然流入出を設定します。また、sideはすべり壁とします。回転領域設定では、回転速度を0とします。
以上の設定で、エクスポートで推進力算出用とは別名で解析ファイルを出力します。
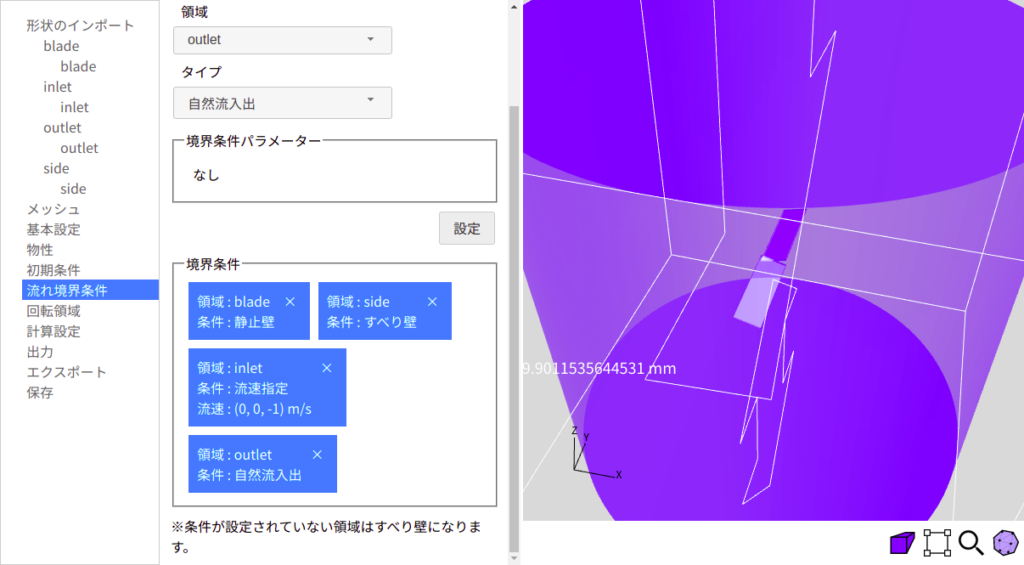
XSimから出力された解析ファイルを展開し、あらかじめ推進力を計算した際に用いた解析ファイルをコピーペーストしたものに、今回出力展開したファイルから0フォルダを上書き保存します。また、コピーペーストした解析ファイルの内、constantフォルダのMRFpropertiesファイル内のomegaを0に変更します。MRFpropertiesファイルについては、いきなりOpenFOAM第69回を参照してください。
以上の修正を行った解析ファイルで、端末からsimpleFoamと入力し計算を実行します。
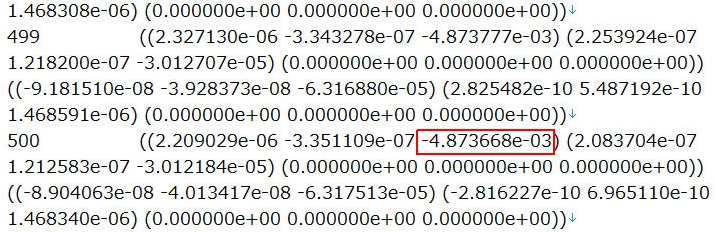
図10に流体抵抗力算出用の設定で計算した縦断面流速分を示します。図を見ると、下向きの気流を受けて、竹とんぼの下流側には渦が発生していることがわかります。流体抵抗力は、postProcessingフォルダ内forces.datファイルをエディタで開き、図11に示す赤い枠で囲まれた数値が流体抵抗力を表しています。

今回は竹とんぼの解析を行い、運動方程式の係数A, B, Cに必要な結果を得ました。
推進力を表す係数Aは単位回転速度(1rad/s)の二乗あたりの推進力、同じく係数Bは単位回転速度の二乗あたりの負荷トルクであるため、図8の赤い枠と青い枠で囲まれた数値を回転速度314rad/sの二乗で割った値が係数AおよびBとなり、推進力の係数がA=4.18×10-6N/(rad/s)2、負荷トルクの係数がB=0.17×10-6 Nm/(rad/s)2と求まります。流体抵抗力の係数Cは単位流速1m/sの二乗あたりの抵抗であり、図11の赤い枠の数値からC=4.87×10-3 N/(m/s)2と求まります。質量mと慣性モーメントIはCADのプロパティ機能を用いて、m=7.69×10-3kg、I=26.15×10-6kgm2となります。
次回は、得られた係数を用いて、運動方程式を数値的に解いてみます。
このページでは、各アプリケーションの操作説明は省略しています。FreeCADの具体的な操作については、いきなりOpenFOAM第5回および第7回、OpenFOAMでの計算実行は第8回、ParaViewの操作については第3回、第4回および第8回を参考にしてみてください。
おことわり
本コンテンツの動作や表示はお使いのバージョンにより異なる場合があります。
本コンテンツの動作ならびに設定項目等に関する個別の情報提供およびサポートはできかねますので、あらかじめご了承ください。
本コンテンツは動作および結果の保証をするものではありません。ご利用に際してはご自身の判断でお使いいただきますよう、お願いいたします。

